题目内容
提高南京长江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数图象如下.当车流密度不超过20辆/千米,此时车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数;当桥上的车流密度达到200辆/千米,造成堵塞,此时车流速度为0.
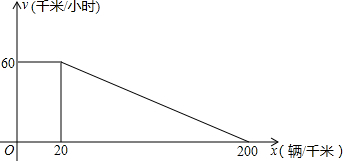
(1)求当20≤x≤200时大桥上的车流速度v与车流密度x的函数关系式.
(2)车流量y(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)满足y=x•v,当车流密度x为多大时,车流量y可以达到最大,并求出最大值.(精确到1辆/小时)

(1)求当20≤x≤200时大桥上的车流速度v与车流密度x的函数关系式.
(2)车流量y(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)满足y=x•v,当车流密度x为多大时,车流量y可以达到最大,并求出最大值.(精确到1辆/小时)
考点:二次函数的应用
专题:
分析:(1)直接利用待定系数法求一次函数解析式得出即可;
(2)分别利用当0≤x≤20时y=60x,当20<x≤200时y=x•v=-
x2+
x 求出一次函数以及二次函数最值即可.
(2)分别利用当0≤x≤20时y=60x,当20<x≤200时y=x•v=-
| 1 |
| 3 |
| 200 |
| 3 |
解答:解:(1)设v=kx+b,把(20,60)(200,0)代入得:
,
解得
.
当20≤x≤200时大桥上的车流速度v与车流密度x的函数关系式为:v=-
x+
;
(2)当0≤x≤20时y=60x 当x=20时y最大为1200辆;
当20<x≤200时y=x•v=-
x2+
x
=-
(x-100)2+
,
当x=100时,y最大为3333辆.
因为3333>1200,
所以当x=100时,y最大为3333辆.
|
解得
|
当20≤x≤200时大桥上的车流速度v与车流密度x的函数关系式为:v=-
| 1 |
| 3 |
| 200 |
| 3 |
(2)当0≤x≤20时y=60x 当x=20时y最大为1200辆;
当20<x≤200时y=x•v=-
| 1 |
| 3 |
| 200 |
| 3 |
=-
| 1 |
| 3 |
| 10000 |
| 3 |
当x=100时,y最大为3333辆.
因为3333>1200,
所以当x=100时,y最大为3333辆.
点评:此题主要考查了二次函数与一次函数应用,利用一次函数增减性以及配方法求出二次函数最值是解题关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
无论k取任何实数,直线y=kx-3k+2上总有一个定点到原点的距离不变,这个距离为( )
A、
| ||
B、
| ||
C、
| ||
D、2
|
对于数据组3,3,2,3,6,3,10,3,6,3,2.这组数据的平均数与众数分别为( )
| A、4,3 | B、3,3 |
| C、4.5,2 | D、5,6 |
 △ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB=
△ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB= 公园里有一块形如四边形ABCD的草地,测得BC=CD=10米,∠B=∠C=120°,∠ADC=75°,请你求出这块草地的面积.
公园里有一块形如四边形ABCD的草地,测得BC=CD=10米,∠B=∠C=120°,∠ADC=75°,请你求出这块草地的面积.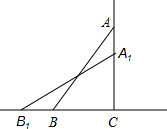 如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数)
如图,一架13米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为5米,如果梯子的顶端沿墙下滑1米,那么梯子将向外移多少米?(保留两位小数) 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.