题目内容
11.(1)已知关于x的方程x2-kx-6=0的一个根为x=3,求另一个根及实数k的值.(2)当k为何值时,关于x的方程kx2-(2k+1)x+k+3=0有两个不相等的实数根?
分析 (1)把x1=3代入已知方程,列出关于k的一元一次方程,通过解方程求得k的值;由根与系数的关系来求方程的另一根即可;
(2)根据方程有两个不相等实数根,得出根的判别式△>0,再建立关于k的不等式,求得k的取值范围,最后根据二次项系数不为零,从而得出答案.
解答 解:(1)∵关于x的一元二次方程x2-kx-6=0的一个根是x1=3,
∴32-3k-6=0,
解得k=1.
又∵x1•x2=-6,即3x2=-6,
∴x2=-2.
综上所述,k的值是1,方程的另一个根是-2;
(2)∵方程kx2-(2k+1)x+k+3=0,有两个不相等的实数根,
∴△=[-(2k+1)]2-4×k(k+3)=-8k+1>0,
∴k<$\frac{1}{8}$,
∴当k<$\frac{1}{8}$且k≠0时方程有两个不相等的实数根.
点评 本题考查了根与系数的关系和根的判别式的知识,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
16.无论a取何值,下列各式中一定有意义的是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{{a^2}-1}$ | C. | a-2 | D. | $\sqrt{{a^2}+1}$ |
3. 如图,根据有理数a,b,c在数轴上的位置,下列关系正确的是( )
如图,根据有理数a,b,c在数轴上的位置,下列关系正确的是( )
 如图,根据有理数a,b,c在数轴上的位置,下列关系正确的是( )
如图,根据有理数a,b,c在数轴上的位置,下列关系正确的是( )| A. | b>c>0>a | B. | a>0>c>b | C. | b>a>c>0 | D. | c<0<a<b |
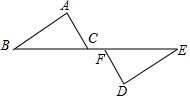 如图,△ABC≌△DEF,点B、F、C、E在同一条直线上.求证:
如图,△ABC≌△DEF,点B、F、C、E在同一条直线上.求证: 如图,△ABC≌△ADE,若∠B=40°,∠EAB=80°,∠C=45°,则∠DAC=90°.
如图,△ABC≌△ADE,若∠B=40°,∠EAB=80°,∠C=45°,则∠DAC=90°. 如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.
如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.