Question

3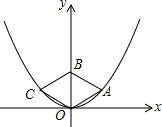．如图，菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x²上，其中点O为坐标原点，对角线OB在y轴上，且OB=2．则菱形OABC的面积是（　　）

• A． 2$\sqrt{2}$
• B． 2$\sqrt{3}$
• C． 4
• D． 4$\sqrt{3}$

Answer 1

分析 根据二次函数图象上点的坐标性质得出A，C点坐标，进而利用三角形面积求法得出答案．

解答 解：∵菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x²上，对角线OB在y轴上，且OB=2，
∴由题意可得：A，C点纵坐标为1，
故1=$\frac{1}{3}$x²，
解得：x=±$\sqrt{3}$，故A（$\sqrt{3}$，1），C（-$\sqrt{3}$，1），
故菱形OABC的面积是：2×（$\frac{1}{2}$×2×$\sqrt{3}$）=2$\sqrt{3}$．
故选：B．

点评 此题主要考查了菱形的性质以及二次函数图象上点的坐标性质，得出A，C点坐标是解题关键．