题目内容
13. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A、点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A、点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
分析 先利用互余计算出∠BAC=30°,再根据含30度的直角三角形三边的关系得到AB=2BC=2,接着根据旋转的性质得A′B′=AB=2,B′C=BC=1,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,于是可判断△CAA′为等腰三角形,所以∠CAA′=∠A′=30°,再利用三角形外角性质计算出∠B′CA=30°,可得B′A=B′C=1,然后利用AA′=AB′+A′B′进行计算.
解答 解:∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴AB=2BC=2×1=2,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=2,B′C=BC=1,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=1,
∴AA′=AB′+A′B′=2+1=3.
故选:A.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
5.加一次暴风雨袭击过后,人们发现一棵9m高的大树被从离地面4m高的地方折断,则树顶与地面的接触点距树根可能是( )
| A. | 1m | B. | 9m | C. | 3m | D. | 13m |
3.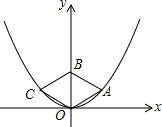 如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
 如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
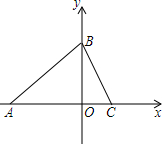 如图,在平面直角坐标系中,点C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.点B到x轴的距离为3.
如图,在平面直角坐标系中,点C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.点B到x轴的距离为3.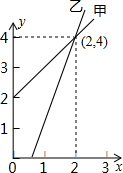 如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:
如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论: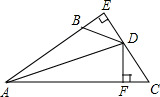 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.