题目内容
18.若方程$\frac{2x-1}{3}=\frac{2x+1}{4}$与关于x的方程4x-$\frac{1}{2}$=2(x+n)的解相同,则n-3的平方根是±$\frac{1}{2}$.分析 根据方程的解相同,可得关于n的方程,根据开平方,可得平方根.
解答 解:解第一个方程得:x=$\frac{7}{2}$,
解第二个方程得:x=$\frac{1}{4}$+n,
∴n+$\frac{1}{4}$=$\frac{7}{2}$,
解得:n=$\frac{13}{4}$.
n-3=$\frac{13}{4}$-3=$\frac{1}{4}$,
n-3的平方根是$±\sqrt{\frac{1}{4}}$=±$\frac{1}{2}$.
故答案为:±$\frac{1}{2}$.
点评 本题考查了同解方程,利用方程的解相同得出关于n的方程是解题关键,又利用了开平方运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列说法正确的是( )
| A. | 一个数不是正数就是负数 | B. | 自然数一定是正数 | ||
| C. | 0是偶数 | D. | 整数是正整数和负整数的统称 |
13.在(-1)2015,|-1|3,-(-1)18,18这四个有理数中,负数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.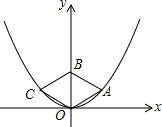 如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
 如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
 如图,在正方形内,截去两个以正方形的边长为直径的半圆.
如图,在正方形内,截去两个以正方形的边长为直径的半圆. 如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).