题目内容
7.在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax+3与x轴负半轴交于A,与x轴的正半轴交于点B,与y轴的正半轴交于点C,且AB=4.(1)如图1,求a的值;
(2)如图2,连接AC,BC,点D在第一象限内抛物线上,过D作DE∥AC,交线段BC于E,若DE=$\sqrt{5}$EC,求点D的坐标;
(3)如图3,在(2)的条件下,连接DC并延长,交x轴于点F,点P在第一象限的抛物线上,连接PF,作CQ⊥PF,交x轴于Q,连接PQ,当∠PQC=2∠PFQ时,求点P的坐标.
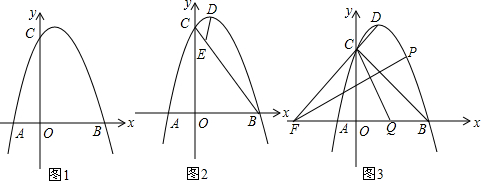
分析 (1)根据抛物线的对称轴x=1,AB=4,求出点A、B坐标,利用待定系数法即可解决问题.
(2)如图2中,作DH⊥AB于H交BC于K,作EM⊥DH于M,交OC于N.设EM=x.想办法表示出点D坐标,代入抛物线的解析式即可解决问题.
(3)如图3中,作PN⊥AB于N,QM⊥AB交BC于M.设P(m,n),想办法列出关于m,n的方程组即可解决问题.
解答 解:(1)∵抛物线的对称轴x=-$\frac{-2a}{2a}$=1,AB=4,
∴A(-1,0),B(3,0),
把A(-1,0)代入抛物线的解析式得a+2a+3=0,
∴a=-1.
(2)如图2中,作DH⊥AB于H交BC于K,作EM⊥DH于M,交OC于N.设EM=x.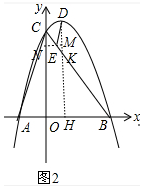
∵AC∥DE,CO∥DM,
∴∠ACO=∠EDM,∵∠AOC=∠EMD,
∴△ACO∽△EDM,
∴$\frac{OA}{EM}$=$\frac{CO}{DM}$,
∴$\frac{1}{x}$=$\frac{3}{DM}$,
∴DM=3x,DE=$\sqrt{E{M}^{2}+D{M}^{2}}$=$\sqrt{10}$x,
∵DE=$\sqrt{5}$CE,
∴EC=$\sqrt{2}$x,
∵OC=OB=3,
∴BC=3$\sqrt{2}$,∠OCB=∠OBC=45°,
∴EN=EM=MK=x,EC=EK=$\sqrt{2}$x,
∴BK=3$\sqrt{2}$-2$\sqrt{2}$x,
∴BH=KH=3-2x,
∴DH=3+2x,
∴D(2x,3+2x)代入y=-x2+2x+3,
3+2x=-4x2+4x+3,
解得x=$\frac{1}{2}$或0(舍弃),
∴D(1,4).
(3)如图3中,作PN⊥AB于N,QM⊥AB交BC于M.设P(m,n).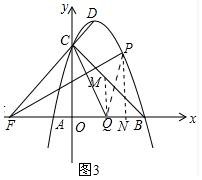
∵C(0,3),D($\frac{1}{2}$,$\frac{15}{4}$),
∴直线CD的解析式为y=$\frac{3}{2}$x+3,
∴F(-2,0)
∵∠OCQ+∠OQC=90°,
∠PFO+∠CQF=90°,
∴∠PFQ=∠OCQ,
∵OC∥QM,
∴∠OCQ=∠CQM,
∵∠CQP=2∠PFQ,
∴∠PQM=∠CQM,
∵QM∥PN,
∴∠MQP=∠QPN,
∴∠QPN=∠NFP,∵∠PNQ=∠PNF,
∴△PNQ∽△FNP,
∴PN2=NQ•NF,
∴NQ=$\frac{{m}^{2}}{n+2}$,OQ=m-$\frac{{m}^{2}}{n+2}$,
∵tan∠OCQ=tan∠PFN,
∴$\frac{m-\frac{{m}^{2}}{m+2}}{3}$=$\frac{m}{n+2}$,
∴n-m=1 ①,
又∵n=-m2+m+3 ②,
由①②可得,$\left\{\begin{array}{l}{m=\sqrt{2}}\\{n=1+\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=-\sqrt{2}}\\{n=1-\sqrt{2}}\end{array}\right.$(舍弃),
∴点P坐标($\sqrt{2}$,1+$\sqrt{2}$).
点评 本题考查二次函数综合题、一次函数、待定系数法、勾股定理、锐角三角函数等知识,解题的关键是灵活运用待定系数法确定函数解析式,学会利用转化的思想思考问题,把问题转化为方程组解决,属于中考压轴题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
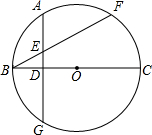 已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.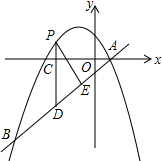 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.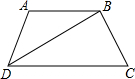 如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.
如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.