题目内容
9. 已知抛物线y=$\frac{1}{2}{x}^{2}$+(m-2)x+2m-6的对称轴为直线x=1,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
已知抛物线y=$\frac{1}{2}{x}^{2}$+(m-2)x+2m-6的对称轴为直线x=1,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)求m的值;
(2)求A,B,C三点的坐标;
(3)过点C作直线l∥x轴,将该抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:当直线y=$\frac{1}{2}x+b$与图象G只有一个公共点时,求b的取值范围.
分析 (1)根据题意得出-m+2=1,求得m=1,
(2)分别令x=0、y=0,得到方程,解方程即可求得;
(3)分两种情况分别讨论即可得出b的取值范围.
解答  解:(1)∵抛物线y=$\frac{1}{2}{x}^{2}$+(m-2)x+2m-6的对称轴为直线x=1,
解:(1)∵抛物线y=$\frac{1}{2}{x}^{2}$+(m-2)x+2m-6的对称轴为直线x=1,
∴-m+2=1,
∴m=1;
(2)令y=0,
∴$\frac{1}{2}{x}^{2}$-x-4=0,解得x=-2或x=4,
∴A(-2,0),B(4,0),
令x=0,则y=-4,
∴C(0,-4);
(3)由图象可知:
①当直线过C(0,-4)时,b=-4,
∴b>-4;
②当直线与抛物线只有应该交点时,∴$\frac{1}{2}{x}^{2}$-x-4=$\frac{1}{2}$x+b,
整理得,x2-3x-8-2b=0,
∵△=9+4(8+2b)=0,
∴b=-$\frac{41}{8}$,
∴b<-$\frac{41}{8}$,
综上,结合图象可知,b的取值范围为b>-4或b<-$\frac{41}{8}$.
点评 本题考查了二次函数的图象与结合变换,抛物线与坐标轴的交点,主要考查学生数形结合的数学思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若顺次连结四边形ABCD各边中点所得四边形是矩形,则原四边形必定是( )
| A. | 正方形 | B. | 对角线相等的四边形 | ||
| C. | 菱形 | D. | 对角线相互垂直的四边形 |
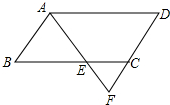 如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度.
如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.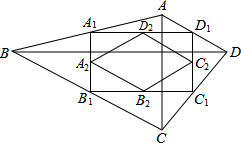 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.