题目内容
15.材料:①1的任何次幂都为1;②-1的奇数次幂为-1;③-1的偶次幂为1;④任何不等于零的数的零次幂都是1,请问当x为何值时,代数式(2x+3)x+2010的值为1?分析 根据题目给出的材料,先计算底数为1的情况;再计算底数为-1,指数为偶数的情况;最后计算指数为0的情况得出结论.
解答 解:(1)由2x+3=1,得x=-1,
当x=-1时,代数式(2x+3)x+2010=12009=1;
(2)由2x+3=-1,得x=-2,
当x=-2时,代数式(2x+3)x+2010=(-1)2008=1;
(3)由x+2010=0,得x=-2010,
当x=-2010时,2x+3=-4017≠0
所以(2x+3)x+2010=(-4017)0=1.
当x=-2010时,代数式(2x+3)x+2010的值为1.
答:当x为-1、-2、-2010时,代数式(2x+3)x+2010的值为1.
点评 本题考查了有理数的乘方及分情况讨论.解决本题的关键是弄清楚代数式值为1的所有情况,然后分别求出x的值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价a元后,再次打7折,现售价为b元,则原售价为( )
| A. | $a+\frac{7b}{10}$ | B. | $a+\frac{10b}{7}$ | C. | $b+\frac{7a}{10}$ | D. | $b+\frac{10a}{7}$ |
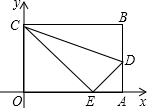 如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.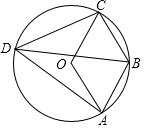 如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°.
如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°. 如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.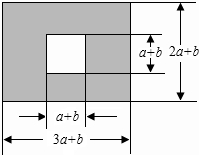 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形广场,规划部门将阴影部分进行绿化,中间边长为(a+b)米的正方形将修建一座雕塑,则:
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形广场,规划部门将阴影部分进行绿化,中间边长为(a+b)米的正方形将修建一座雕塑,则: