题目内容
2.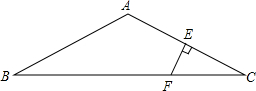 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
分析 连接AF,求出CF=AF,∠BAF=90°,再根据AB=AC,∠BAC=120°可求出∠B的度数,由直角三角形的性质即可求出BF=2AF=2CF,于是得到结论.
解答  解:BF=2CF.
解:BF=2CF.
证明:连接AF,
∵AB=AC,∠BAC=120°
∴∠B=∠C=30°,
∵EF垂直平分AC,
∴AF=CF,
∴∠CAF=∠C=30°,
∴∠AFB=∠CAF+∠C=60°,
∴∠BAF=180°-∠B-∠AFB=90°,
∴BF=2AF,
∴BF=2CF.
点评 本题考查的是线段垂直平分线的性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.将一个直角三角形绕它的一条直角边旋转一周得到的几何体是 ( )
| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 圆台 |
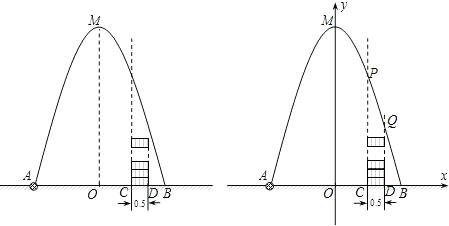
10. 如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
 如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )
如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
12.位于江汉平原的兴隆水利枢纽工程于2014年9月25日竣工,该工程设计的年发电量为2.25亿度,那么这个数值( )
| A. | 精确到亿位 | B. | 精确到百分位 | C. | 精确到千万位 | D. | 精确到百万位 |
 如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想. 如图,直线y=kx+8分别与x轴,y轴相交于A,B两点,O为坐标原点,A点的坐标为(4,0).
如图,直线y=kx+8分别与x轴,y轴相交于A,B两点,O为坐标原点,A点的坐标为(4,0). 如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为(2,5).
如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为(2,5).