题目内容
13. 如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM等于( )
如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM等于( )| A. | 0.5 | B. | 1 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 过点M作MG⊥AC,垂足为G.依据圆周角定理可知∠C=90°,然后依据含30度直角三角形的性质可求得AC=1,然后依据切线长定理可求得AM=MC,依据等腰三角形三线合一的性质可求得AG=0.5,接下来,再依据切线的性质可求得∠MAB=90°,然后可求得∠DAG=30°,最后在Rt△AMG中利用特殊锐角三角函数值求解即可.
解答 解:过点M作MG⊥AC,垂足为G.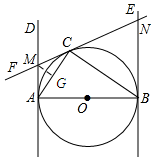
∵AB为⊙O的直径,
∴∠C=90°.
又∵∠ABC=30°,AB=2,
∴AC=1,∠CAB=60°.
∵AD为⊙O的切线,
∴∠DAB=90°.
∴∠MAC=30°.
由切线长定理可知MC=MA.
又∵MG⊥AC,
∴AG=$\frac{1}{2}$AC=$\frac{1}{2}$.
在Rt△AMG中,∠MAG=30°,
∴$\frac{AG}{AM}$=$\frac{\sqrt{3}}{2}$,即$\frac{0.5}{AM}=\frac{\sqrt{3}}{2}$,解得:AM=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题主要考查的是切线的性质、切线长定理、圆周角定理、直角三角形的性质、特殊锐角三角函数值的应用,求得∠AMG的度数以及AG的长是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.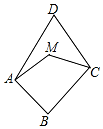 如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )
如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )
 如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )
如图,M是线段AD、CD的垂直平分线交点,AB⊥BC,∠D=55°,则∠MAB+∠MCB的大小是( )| A. | 120° | B. | 130° | C. | 140° | D. | 160° |