题目内容
5.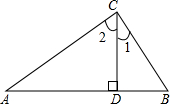 如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)
如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)①∠1=∠A;②c•h=a•b;③∠A=∠2;④a:b:c=3:4:5.
分析 由CD垂直AB于D,由等量代换的知识,易得由①∠1=∠A,可判定△ABC为直角三角形;由相似三角的判定与性质,②c•h=a•b,可判定△ABC为直角三角形,根据③∠A=∠2只能判断△ADC是等腰直角三角形;由勾股定理的逆定理,由④a:b:c=3:4:5,可判定△ABC为直角三角形.
解答 解:∵CD⊥AB于D,
∴∠1+∠B=90°,
∵∠1=∠A,
∴∠A+∠B=90°,
∴∠ACB=90°,故①正确;
∵c•h=a•b,
∴$\frac{AB}{BC}=\frac{AC}{CD}$,
∵∠B=∠B,
∴△ABC∽△BCD,
∴∠ACB=∠CDB=90°,故②正确;
∵CD⊥AB于D,∠A=∠2,
∴∠A=∠2=45°,
但AC≠BC,
∴∠B不一定等于45°,
∴∠ACB不一定等于90°,故③错误;
∵a:b:c=3:4:5,
∴设BC的长为3x,那么AC为4x,AB为5x,由9x2+16x2=25x2,符合勾股定理的逆定理,故④正确.
故答案为:①②④.
点评 此题主要考查直角三角形的判定及相似三角形的判定方法的运用.通过证明把题目中的条件进行转化是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
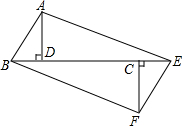 如图,已知△ABD和△CEF都是斜边长为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E在同一直线上,DC=4.
如图,已知△ABD和△CEF都是斜边长为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E在同一直线上,DC=4.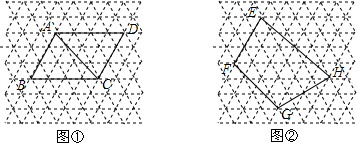
 如图,已知△ABC是等边三角形,BE=CD,EH⊥AD于H,DG∥EH交CE于G,求证:EG=2HD.
如图,已知△ABC是等边三角形,BE=CD,EH⊥AD于H,DG∥EH交CE于G,求证:EG=2HD.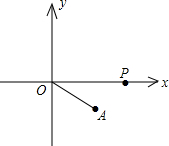 如图,坐标平面内一点A(4,-3),O为原点,P是x轴上的一个动点,如果以点P,O,A为顶点的三角形是等腰三角形,那么不经过第一象限的直线PA的解析式为y=-$\frac{1}{3}$x-$\frac{5}{3}$.
如图,坐标平面内一点A(4,-3),O为原点,P是x轴上的一个动点,如果以点P,O,A为顶点的三角形是等腰三角形,那么不经过第一象限的直线PA的解析式为y=-$\frac{1}{3}$x-$\frac{5}{3}$.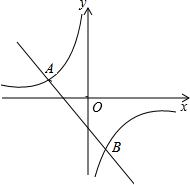 如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.
如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.