题目内容
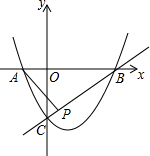 已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.
已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.考点:二次函数综合题
专题:压轴题
分析:利用抛物线解析式求出点A、B的坐标,再把点P的坐标代入直线求出k值,设点M的坐标为(a,0),根据平行四边形的对边平行且相等分点N在点M的右边和左边两种情况表示出点N的坐标,然后代入抛物线解析式求出a的值,即可得解.
解答: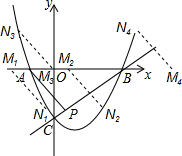 解:令y=0,则x2-2x-3=0,
解:令y=0,则x2-2x-3=0,
解得x1=-1,x2=3,
所以,A(-1,0),B(3,0),
∵点P(1,k)在y=x-3上,
∴k=1-3=-2,
∴点P(1,-2),
设点M的坐标为(a,0),若点N在点M的右边,则N(a+2,-2),
代入抛物线得,(a+2)2-2(a+2)-3=-2,
a1=-1-
,a2=-1+
,
此时,点M1(-1-
,0),M2(-1+
,0),
若点N在点M的左边,则点N(a-2,2),
代入抛物线得,(a-2)2-2(a-2)-3=2,
a1=3-
,a2=3+
,
此时,点M3(3-
,0),M4(3-
,0),
综上所述,存在点M1(-1-
,0),M2(-1+
,0),M3(3-
,0),M4(3-
,0),使以点A、M、N、P为顶点的四边形为平行四边形.
 解:令y=0,则x2-2x-3=0,
解:令y=0,则x2-2x-3=0,解得x1=-1,x2=3,
所以,A(-1,0),B(3,0),
∵点P(1,k)在y=x-3上,
∴k=1-3=-2,
∴点P(1,-2),
设点M的坐标为(a,0),若点N在点M的右边,则N(a+2,-2),
代入抛物线得,(a+2)2-2(a+2)-3=-2,
a1=-1-
| 2 |
| 2 |
此时,点M1(-1-
| 2 |
| 2 |
若点N在点M的左边,则点N(a-2,2),
代入抛物线得,(a-2)2-2(a-2)-3=2,
a1=3-
| 6 |
| 6 |
此时,点M3(3-
| 6 |
| 6 |
综上所述,存在点M1(-1-
| 2 |
| 2 |
| 6 |
| 6 |
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点问题,一次函数图象上点的坐标特征,二次函数图象上点的坐标特征,平行四边形的性质,根据平行四边形的性质用点M的坐标表示出点N的坐标是解题的关键,难点在于分情况讨论.

练习册系列答案
相关题目
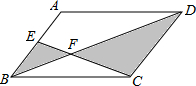 如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积.
如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积. 学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y与另一边x之间的函数关系式如图所示.
学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y与另一边x之间的函数关系式如图所示. 用AB两种规格的长方形纸板(如图①)无重合,无缝隙地拼接可得到如图②所示的周长为28cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积为
用AB两种规格的长方形纸板(如图①)无重合,无缝隙地拼接可得到如图②所示的周长为28cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积为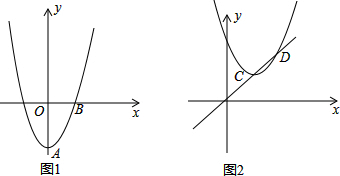
 已知:如图,线段AB=16cm,E为AB的中点,C为AB上一点,D为AB延长线上的点,且CD=4cm,B为CD的中点.求线段EC和ED的长.
已知:如图,线段AB=16cm,E为AB的中点,C为AB上一点,D为AB延长线上的点,且CD=4cm,B为CD的中点.求线段EC和ED的长.