题目内容
 学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y与另一边x之间的函数关系式如图所示.
学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边y与另一边x之间的函数关系式如图所示.(1)绿化带的面积是多少?你能写出这个函数的表达式吗?
(2)如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内?
考点:反比例函数的应用
专题:
分析:(1)矩形绿化带的面积为定值且满足反比例函数的关系,代入A点的坐标即可求得绿化带的面积和函数关系式;
(2)代入x=40求得y值即可确定宽的取值范围.
(2)代入x=40求得y值即可确定宽的取值范围.
解答:解:(1)设函数关系式为y=
,
∵经过点A(40,10),
∴k=40×10=400,
∴矩形的面积为400平方米,函数关系式为y=
;
(2)∵该绿化带的长不得超过40m,
∴当x=40时y=10,
∴它的宽应控制在10-20米之间.
| k |
| x |
∵经过点A(40,10),
∴k=40×10=400,
∴矩形的面积为400平方米,函数关系式为y=
| 400 |
| x |
(2)∵该绿化带的长不得超过40m,
∴当x=40时y=10,
∴它的宽应控制在10-20米之间.
点评:本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数的模型,难度不大.

练习册系列答案
相关题目
关于x的方程(k+4)x2-2=0是关于x的一元二次方程,则k的取值范围是( )
| A、k≠0 | B、k≥4 |
| C、k=-4 | D、k≠-4 |
下列方程:①5x=6x-7y;②
+x=1;③x2=3x;④x=0;⑤2x-5=7.其中,属于一元一次方程的有( )
| 8 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
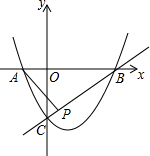 已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.
已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.