题目内容
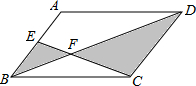 如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积.
如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积.考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:如图,作辅助线;得到SABCD=CD•AG=4;证明△BEF∽△DCF,利用相似三角形的性质,求出△BEF,△DFC面积之间的数量关系;借助面积公式求出△BDC的面积,进而求出△BEF与△DCF的面积,问题即可解决.
解答: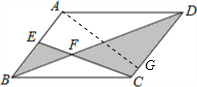 解:如图,过点A作AE⊥CD于点G;
解:如图,过点A作AE⊥CD于点G;
∵四边形ABCD为平行四边形,
∴CD=AB,SABCD=CD•AG=4;,
∵E为AB的中点,
∴BE=
AB=
CD,
∵AB∥CD,
∴△BEF∽△DCF,
∴
=
=
,
=(
)2;
=
=
∵S△BCD=
CD•AG=2,
∴S△DCF=
×2=
,S△BEF=
×
=
,
∴图中阴影部分的面积=
+
=
,
即图中阴影部分的面积为
.
 解:如图,过点A作AE⊥CD于点G;
解:如图,过点A作AE⊥CD于点G;∵四边形ABCD为平行四边形,
∴CD=AB,SABCD=CD•AG=4;,
∵E为AB的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴△BEF∽△DCF,
∴
| BF |
| DF |
| BE |
| CD |
| 1 |
| 2 |
| S△BEF |
| S△DCF |
| 1 |
| 2 |
| S△BCF |
| S△DCF |
| BF |
| DF |
| 1 |
| 2 |
∵S△BCD=
| 1 |
| 2 |
∴S△DCF=
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 4 |
| 4 |
| 3 |
| 1 |
| 3 |
∴图中阴影部分的面积=
| 4 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
即图中阴影部分的面积为
| 5 |
| 3 |
点评:该命题以平行四边形为载体,以考查平行四边形的性质、平行四边形的面积公式为核心构造而成;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
相关题目
关于x的方程(k+4)x2-2=0是关于x的一元二次方程,则k的取值范围是( )
| A、k≠0 | B、k≥4 |
| C、k=-4 | D、k≠-4 |
 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A、
| ||
B、5
| ||
| C、13cm | ||
D、
|
下列方程:①5x=6x-7y;②
+x=1;③x2=3x;④x=0;⑤2x-5=7.其中,属于一元一次方程的有( )
| 8 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知AB=AC,AB+BC=20,AB的垂直平分线MN交AC于点D,则△BDC的周长为
如图,已知AB=AC,AB+BC=20,AB的垂直平分线MN交AC于点D,则△BDC的周长为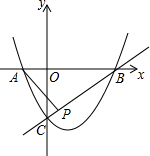 已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.
已知抛物线y=x2-2x-3经过A、B、C三点,点P(1,k)在直线BC:y=x-3上,若点M在x轴上,点N在抛物线上,是否存在以点A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标.