题目内容
4.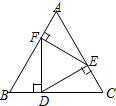 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )| A. | 1:3 | B. | 2:3 | C. | $\sqrt{3}$:2 | D. | $\sqrt{3}$:3 |
分析 首先根据题意求得:∠DFE=∠FED=∠EDF=60°,即可证得△DEF是正三角形,又由直角三角形中,30°所对的直角边是斜边的一半,得到边的关系,即可求得DF:AB=1:$\sqrt{3}$,又由相似三角形的面积比等于相似比的平方,即可求得结果.
解答 解:∵△ABC是正三角形,
∴∠B=∠C=∠A=60°,
∵DE⊥AC,EF⊥AB,FD⊥BC,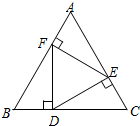
∴∠AFE=∠CED=∠BDF=90°,
∴∠BFD=∠CDE=∠AEF=30°,
∴∠DFE=∠FED=∠EDF=60°,$\frac{BD}{BF}$=$\frac{1}{2}$,
∴△DEF是正三角形,
∴BD:DF=1:$\sqrt{3}$①,BD:AB=1:3②,△DEF∽△ABC,
①÷②,$\frac{AB}{DF}$=$\sqrt{3}$,
∴DF:AB=1:$\sqrt{3}$,
∴△DEF的面积与△ABC的面积之比等于1:3.
故选:A.
点评 此题考查了相似三角形的判定与性质,以及直角三角形的性质.此题难度不是很大,解题时要注意仔细识图.

练习册系列答案
相关题目
15.m和5的和的一半是正数,用不等式表示( )
| A. | m+$\frac{5}{2}$>0 | B. | $\frac{1}{2}$(m+5)≥0 | C. | $\frac{1}{2}$(m+5)>0 | D. | $\frac{1}{2}$(m+5)<0 |
16.关于x的方程kx2-3x-1=0有实根,则k的取值范围是( )
| A. | k$≤-\frac{9}{4}$ | B. | k$≥-\frac{9}{4}$且k≠0 | C. | k$≥-\frac{9}{4}$ | D. | k>$-\frac{9}{4}$且k≠0 |
14.用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面圆的半径是( )
| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |

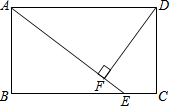 在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.