题目内容
5.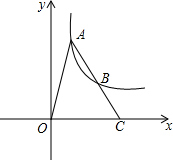 如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点.
如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点.(1)求k的值;
(2)求点B的坐标;
(3)求△OAC的面积.
分析 (1)把A的坐标代入y=$\frac{k}{x}$,即可求得k的值;
(2)根据A的坐标求得B的纵坐标为2,代入y=$\frac{4}{x}$求得x=2,即可求得B的坐标;
(3)根据A、B的坐标求得直线AB的解析式,求得C的坐标,然后根据三角形面积公式即可求得.
解答 解:(1)把A(1,4)代入y=$\frac{k}{x}$得4=$\frac{k}{1}$,
解得k=4;
(2)由B是AC的中点可得B点的纵坐标是A点纵坐标的一半,即y=2,
把y=2代入y=$\frac{4}{x}$求得x=2,故B点的坐标为(2,2);
(3)由A、B点的坐标求得直线AB的解析式为y=-2x+6,
令y=0,求得x=3,
∴C点的坐标为(3,0)
∴△OAC的面积为$\frac{1}{2}$×3×4=6.
点评 本题考查了待定系数法求反比例函数和一次函数的解析式的解析式,反比例函数图象上点的坐标特征,三角形面积等,求得B点的坐标是解题的关键.

练习册系列答案
相关题目
13.在-22,-(-2),+(-$\frac{1}{2}$),-|-2|,(-2)2这五个数中,负数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.计算0-2+4-6+8所得的结果是( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
15.已知一个等腰三角形两边长分别为5,6,那么它的周长为( )
| A. | 16 | B. | 17 | C. | 16或17 | D. | 10或12 |