题目内容
若将抛物线y=-x2+2x-2先向右平移一个单位，再沿x轴翻折到第一象限，然后向右平移一个单位，再沿y轴翻折到第二象限，…，以此类推，如果把向右平移一个单位，再沿一条坐标轴翻折一次记作1次变换，那么拋物线y=-x2-2x-2经过第50次变换后，所得抛物线的函数解析式为（ ）
| A、y=（x+3）2+1 |
| B、y=（x-2）2+1 |
| C、y=-（x+2）2-1 |
| D、y=-（x+3）2+1 |
考点：二次函数图象与几何变换
专题：规律型
分析：把抛物线解析式整理成顶点式形式并写出顶点坐标，然后判断出每4次变换为一个循环组循环，用50÷4，根据商和余数的情况确定出第50次变换后的抛物线所在的象限以及顶点坐标，然后利用顶点式解析式写出即可．
解答：解：∵y=-x2+2x-2=-（x-1）2-1，
∴原抛物线的顶点坐标为（1，-1），
第1次变换，顶点坐标为（2，1），
第2次变换，顶点坐标为（-3，1），
第3次变换，顶点坐标为（-2，-1），
第4次变换，顶点坐标为（1，-1），
…，
以此类推，每4次变换为一个循环组循环，
∵50÷4=12余2，
∴第50次变换与第二次变换相同，
∴经过第50次变换后，所得抛物线的函数解析式为y=（x+3）2+1．
故选A．
∴原抛物线的顶点坐标为（1，-1），
第1次变换，顶点坐标为（2，1），
第2次变换，顶点坐标为（-3，1），
第3次变换，顶点坐标为（-2，-1），
第4次变换，顶点坐标为（1，-1），
…，
以此类推，每4次变换为一个循环组循环，
∵50÷4=12余2，
∴第50次变换与第二次变换相同，
∴经过第50次变换后，所得抛物线的函数解析式为y=（x+3）2+1．
故选A．
点评：本题考查了二次函数图象与几何变换，利用顶点的变化确定函数解析式的变化求解更简便，本题关键在于求出每4次变换为一个循环组循环．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，∠B、∠C的角平分线交于O，若∠BOC=α，则∠A为（ ）
| A、α-90° |
| B、2α+90° |
| C、2α-180° |
| D、2α+180° |
下列计算正确的是（ ）
| A、2a+3b=5ab |
| B、5y2-3y2=3 |
| C、-p2-p2=-2p2 |
| D、7mn-7=mn |
数据0.000056用科学记数法表示为（ ）
| A、56×10-5 |
| B、5.6×10-5 |
| C、5.6×10-4 |
| D、5.6×105 |
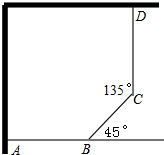用30m长的篱笆和相邻两面墙围成如图形状的小花园，其中AB=CD．设BC=x（m），小花园的面积为S（m2）．求：
如图，等腰△ABC中，AB=AC，以AB为直径的半圆交BC于点D，交AC于点E，已知