题目内容
 如图,等腰△ABC中,AB=AC,以AB为直径的半圆交BC于点D,交AC于点E,已知
如图,等腰△ABC中,AB=AC,以AB为直径的半圆交BC于点D,交AC于点E,已知 |
| DE |
 |
| AE |
考点:圆周角定理,等腰三角形的性质,圆心角、弧、弦的关系
专题:
分析:首先连接AD,由等腰△ABC中,AB=AC,以AB为直径的半圆交BC于点D,可得∠BAD=∠CAD,即可得
=
,继而求得∠BAC的度数,则可求得
的度数.
 |
| BD |
 |
| DE |
 |
| AE |
解答: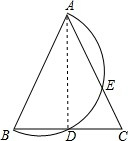 解:连接AD,
解:连接AD,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,
∴
=
=40°,
∴∠BAD=∠CAD=
×40°=20°,
∴∠BAC=40°,
∴∠B=∠C=70°,
∴
=140°,
∴
=
-
=100°.
 解:连接AD,
解:连接AD,∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| DE |
∴∠BAD=∠CAD=
| 1 |
| 2 |
∴∠BAC=40°,
∴∠B=∠C=70°,
∴
 |
| AD |
∴
 |
| AE |
 |
| AC |
 |
| DE |
点评:此题考查了圆周角定理以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若将抛物线y=-x2+2x-2先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限,…,以此类推,如果把向右平移一个单位,再沿一条坐标轴翻折一次记作1次变换,那么拋物线y=-x2-2x-2经过第50次变换后,所得抛物线的函数解析式为( )
| A、y=(x+3)2+1 |
| B、y=(x-2)2+1 |
| C、y=-(x+2)2-1 |
| D、y=-(x+3)2+1 |
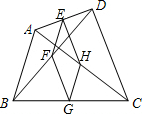 在四边形ABCD中,E、G分别是AD、BC的中点,F、H分别是BD、AC的中点.
在四边形ABCD中,E、G分别是AD、BC的中点,F、H分别是BD、AC的中点. 如图,在正方形ABCD中,E和F分别是BC和CD上的点,AG⊥EF,∠EAF=45°,求证:AG=AD.
如图,在正方形ABCD中,E和F分别是BC和CD上的点,AG⊥EF,∠EAF=45°,求证:AG=AD.