题目内容
2.如图,在圆形纸片和三角形纸片中都刚好能裁剪出棱长为acm的正方体纸盒的表面,那么两种纸片的利用率(纸片利用率=$\frac{纸片被利用的面积}{纸片的总面积}$×100%)的大小关系为( )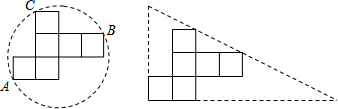
| A. | 圆形纸片利用率大 | B. | 三角形纸片利用率大 | ||
| C. | 两种纸片的利用率一样 | D. | 利用率与a的值有关,无法判断 |
分析 (1)连接AC、BC、AB,根据每个小正方形的边长为a,可以证得∠ACB=90°,故问题可求.
(2)如图2,作辅助线,利用三角形全等和三角形相似对应边成比例,可以分别求得直角三角形的两个直角边的长度,于是问题可求.
解答 解:(1)如图1连接AC,BC,AB, ∴AC=BC=$\sqrt{{a}^{2}{+(3a)}^{2}}$=$\sqrt{10}$a,AB=$\sqrt{{(4a)}^{2}{+(2a)}^{2}}$=$\sqrt{20}$a,
∴AC=BC=$\sqrt{{a}^{2}{+(3a)}^{2}}$=$\sqrt{10}$a,AB=$\sqrt{{(4a)}^{2}{+(2a)}^{2}}$=$\sqrt{20}$a,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴AB是圆的直径,
∴37.5%<38.2%,
故方案一中纸片的利用率高.∴圆形纸片的利用率=$\frac{{6a}^{2}}{{(\sqrt{5}a)}^{2}π}$×100%=$\frac{6}{5π}$×100%=38.2%
由题意,可得△ADE≌△EHF(ASA),
∴AD=EH=1.
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,
∴$\frac{a}{4a}$=$\frac{2a}{BC}$,
∴BC=8a,
∴S△ABC=16a2,
∴三角形字片的面积=$\frac{{6a}^{2}}{{16a}^{2}}$×100%=37.5%,
∵38.2%>37.5%,
∴圆形纸片的利用率大.
故选A.
点评 本题主要考查了圆的面积、三角形的面积的求法,正方体的表面积,三角形全等以及三角形相似等知识点.本题的解答关键是灵活运用所学相关的知识点来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.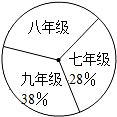 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )| 图书种类 | 频数 | 频率 |
| 科普知识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其它 | 144 | 0.06 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.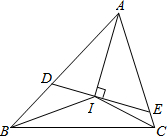 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
| ∠BAC的度数 | 60° | 100° |
| ∠BIC的度数 | 120° | 140° |
| ∠BDI的度数 | 120° | 140° |
7.下列各数中,绝对值最小的数是( )
| A. | -1 | B. | π-3 | C. | 0.3 | D. | -$\sqrt{1.2}$ |
11.($\frac{2}{3}$)1992×(1.5)1991×(-1)1993的结果是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
 如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.
如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积. 将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则192表示的有序实数对是(20,2).
将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则192表示的有序实数对是(20,2).