题目内容
10．
如图，AB∥CD，∠D=75°，∠CAD：∠BAC=2：1，则∠CAD=70．
分析 先根据平行线的性质求出∠BAD的度数，再由∠CAD：∠BAC=2：1即可得出结论．
解答 解：∵AB∥CD，∠D=75°，
∴∠BAD=180°-75°=105°．
∵∠CAD：∠BAC=2：1，
∴∠CAD=$\frac{2}{3}$∠BAD=$\frac{2}{3}$×105°=70°．
故答案为：70．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
相关题目
18．
如图，在△ABC中，∠ACB=90°，D为AB的中点，E为AC上一点，连接DE，并过点D作FD⊥ED，垂足为D，交BC于点F．若AC=BC=14，AE：EC=4：3，则tan∠EFC的值为（ ）
如图，在△ABC中，∠ACB=90°，D为AB的中点，E为AC上一点，连接DE，并过点D作FD⊥ED，垂足为D，交BC于点F．若AC=BC=14，AE：EC=4：3，则tan∠EFC的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
如图，在平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则平行四边形ABCD的周长为18．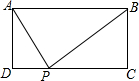
如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP=1或4或2.5．