题目内容
如图①是一个长为2m,宽为2n的长方形(m>n),沿图中虚线用剪刀均匀分民四块小长方形,然后按图②的形状拼成一个正方形.
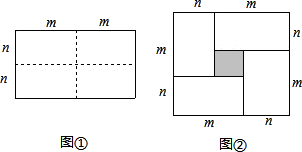
(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.

(1)图②中阴影部分的正方形的边长是多少?(用代数式表示)
(2)观察图②写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系.
(3)若m+n=7,mn=6,求m-n.
考点:列代数式,代数式求值
专题:
分析:(1)观察图形,直接列出代数式即可解决问题.
(2)观察所给的三个代数式的结构特点,直接列出等量关系式即可解决问题.
(3)运用(2)中得到的关系式,直接求出m-n即可解决问题.
(2)观察所给的三个代数式的结构特点,直接列出等量关系式即可解决问题.
(3)运用(2)中得到的关系式,直接求出m-n即可解决问题.
解答:解:(1)图②中阴影部分的正方形的边长是m-n.
(2)(m+n)2=(m-n)2+4mn.
(3)∵(m+n)2=(m-n)2+4mn,且m+n=7,mn=6,
∴m-n=5或-5(舍去).
即m-n=5.
(2)(m+n)2=(m-n)2+4mn.
(3)∵(m+n)2=(m-n)2+4mn,且m+n=7,mn=6,
∴m-n=5或-5(舍去).
即m-n=5.
点评:该题主要考查了运用列代数式来探索图形中隐含的数量关系问题;数形结合是解决这类问题的基础和关键.

练习册系列答案
相关题目
对于任何整数a,多项式(3a+5)2-4都能( )
| A、被9整除 |
| B、被a整除 |
| C、被a+1整除 |
| D、被a-1整除 |
 如图,在平面直角坐标系xOy中,O是坐标原点,已知A(3,2),B(-2,3),则∠OAB等于
如图,在平面直角坐标系xOy中,O是坐标原点,已知A(3,2),B(-2,3),则∠OAB等于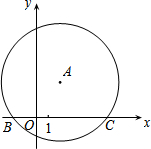 如图,在平面直角坐标系xOy中,以点A(2,3)为圆心的⊙A交x轴于点B,C,BC=8,求⊙A的半径.
如图,在平面直角坐标系xOy中,以点A(2,3)为圆心的⊙A交x轴于点B,C,BC=8,求⊙A的半径. 在某广场儿童游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是2m.
在某广场儿童游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是2m.