题目内容
已知如图1,在以O为原点的平面直角坐标系中,抛物线y=
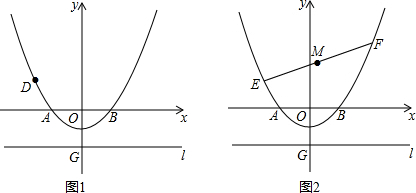
x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,-1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<-1,
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y=
x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.
| 1 |
| 4 |
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y=
| 1 |
| 4 |
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.

考点:二次函数综合题
专题:
分析:(1)根据点C坐标,可得c=-1,然后根据AO=2CO,可得出点A坐标,将点A坐标代入求出b值,即可得出函数解析式;
(2)假设存在直线l使得点D到直线l的距离与OD的长恒相等,设出点D坐标,分别求出OD和点D到直线l的距离,然后列出等式求出t的值;
(3)作EN⊥直线l于点G,FH⊥直线l于点H,设出点E、F坐标,表示出点M的纵坐标,根据(2)中得出的结果,代入结果求出M纵坐标的最小值.
(2)假设存在直线l使得点D到直线l的距离与OD的长恒相等,设出点D坐标,分别求出OD和点D到直线l的距离,然后列出等式求出t的值;
(3)作EN⊥直线l于点G,FH⊥直线l于点H,设出点E、F坐标,表示出点M的纵坐标,根据(2)中得出的结果,代入结果求出M纵坐标的最小值.
解答:解:(1)∵c(0,-1),
∴y=
x2+bx-1,
又∵AO=2OC,
∴点A坐标为(-2,0),
代入得:1-2b-1=0,
解得:b=0,
∴解析式为:y=
x2-1;
(2)假设存在直线l使得点D到直线l的距离与OD的长恒相等,
设D(a,
a2-1),
则OD=
=
=
a2+1,
点D到直线l的距离:
a2-1+|t|,
∴
a2-1+|t|=
a2+1,
解得:|t|=2,
∵t<-1,
∴t=-2,
故当t=-2时,直线l使得点D到直线l的距离与OD的长恒相等;
(3)作EN⊥直线l于点N,FH⊥直线l于点H,
设E(x1,y1),F(x2,y2),
则EN=y1+2,FH=y2+2,
∵M为EF中点,
∴M纵坐标为:
=
=
-2,
由(2)得:EN=OE,FH=OF,
∴
=
-2=
-2,
要使M纵坐标最小,即
-2最小,
当EF过点O时,OE+OF最小,最小值为8,
∴M纵坐标最小值为
-2=
-2=2.
∴y=
| 1 |
| 4 |
又∵AO=2OC,
∴点A坐标为(-2,0),
代入得:1-2b-1=0,
解得:b=0,
∴解析式为:y=
| 1 |
| 4 |
(2)假设存在直线l使得点D到直线l的距离与OD的长恒相等,
设D(a,
| 1 |
| 4 |
则OD=
a2+(
|
(
|
| 1 |
| 4 |
点D到直线l的距离:
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 4 |
解得:|t|=2,
∵t<-1,
∴t=-2,
故当t=-2时,直线l使得点D到直线l的距离与OD的长恒相等;
(3)作EN⊥直线l于点N,FH⊥直线l于点H,

设E(x1,y1),F(x2,y2),
则EN=y1+2,FH=y2+2,
∵M为EF中点,
∴M纵坐标为:
| y1+y2 |
| 2 |
| (EN-2)+(FH-2) |
| 2 |
| EN+FH |
| 2 |
由(2)得:EN=OE,FH=OF,
∴
| y1+y2 |
| 2 |
| EN+FH |
| 2 |
| OE+OF |
| 2 |
要使M纵坐标最小,即
| OE+OF |
| 2 |
当EF过点O时,OE+OF最小,最小值为8,
∴M纵坐标最小值为
| OE+OF |
| 2 |
| 8 |
| 2 |
点评:本题考查了二次函数的综合知识,涉及到抛物线解析式的求法,点到直线的距离、两点间的距离等知识,涉及到的知识点比较多,难度比较大,是中考中的压轴题.特别是存在性问题更是近几年中考的高频考点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程x2-9=0的根是( )
| A、3 | B、±3 | C、9 | D、±9 |
 已知,如图,点B,C,E在一条直线上,AB⊥BE,DE⊥BE,且AB=CE,BC=DE.
已知,如图,点B,C,E在一条直线上,AB⊥BE,DE⊥BE,且AB=CE,BC=DE.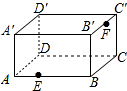 如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )
如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒,则蚂蚁沿长方体表面爬到米粒处的最短距离为( )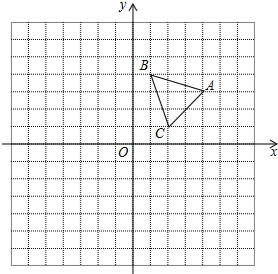 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,3)、B(1,4)、C(2,1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,3)、B(1,4)、C(2,1).