题目内容
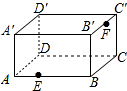如图是放在地面上的一个长方体盒子，其中AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，B′C′中点F处有一米粒，则蚂蚁沿长方体表面爬到米粒处的最短距离为（ ）| A、10 | ||
B、
| ||
C、5+3
| ||
D、6+
|
考点：平面展开-最短路径问题
专题：
分析：利用平面展开图有两种情况，画出图形利用勾股定理求出EF的长即可．
解答：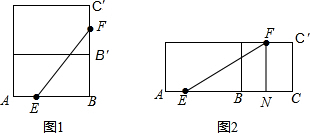
解：如图1，
∵AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，B′C′中点F处有一米粒，
∴BE=6，BF=5+3=8，
∴EF=
=10；
如图2，∵AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，
B′C′中点F处有一米粒，
∴BE=6，EN=9，FN=5，
∴EF=
=
．
∵10＜
，
∴蚂蚁沿长方体表面爬到米粒处的最短距离为10．
故选A．
解：如图1，∵AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，B′C′中点F处有一米粒，
∴BE=6，BF=5+3=8，
∴EF=
| 62+82 |
如图2，∵AB=9，BB′=5，B′C′=6，在线段AB的三等分点E（靠近点A）处有一只蚂蚁，
B′C′中点F处有一米粒，
∴BE=6，EN=9，FN=5，
∴EF=
| 92+25 |
| 106 |
∵10＜
| 106 |
∴蚂蚁沿长方体表面爬到米粒处的最短距离为10．
故选A．
点评：此题主要考查了平面展开图的最短路径问题和勾股定理的应用，利用展开图有两种情况分析得出是解题关键．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
如图，直线AD，BC相交于点O，AB∥CD，AO：AD=2：5，若△AOB的周长为12，求△COD周长．已知y=ax2-2x+1与x轴没有交点，那么该抛物线的顶点在第（ ）象限．
| A、一 | B、二 | C、三 | D、四 |
如图△ABD，△AEC都是等边三角形，求证：
如图，AB∥CD，AB=CD，BE=DF，则图中有多少对全等三角形（ ）| A、3 | B、4 | C、5 | D、6 |
将下列各数在数轴上表示并用“＜”连接起来．