题目内容
16.火星有两颗非常小的卫星,较大卫星的直径为27km,较小卫星的体积是较大卫星体积的$\frac{125}{729}$,求较小卫星的直径(球的体积公式为V=$\frac{4}{3}$πR3,其中V为体积,R为半径)分析 设较小卫星的直径为d.由题意可知;$\frac{{V}_{小}}{{V}_{大}}=\frac{{d}^{3}}{2{7}^{3}}=\frac{125}{729}$,从而可解得较小卫星的直径.
解答 解:设较小卫星的直径为d.
由球体的体积公式可知:${V}_{大}=\frac{4}{3}π×(\frac{27}{2})^{3}$,${V}_{小}=\frac{4}{3}π×(\frac{d}{2})^{3}$,
由题意得:$\frac{{V}_{小}}{{V}_{大}}=\frac{{d}^{3}}{2{7}^{3}}=\frac{125}{729}$,
解得:d=15km.
点评 本题主要考查的是立方根的应用,利用球的体积公式,结合题意列出比例式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列各点在反比例函数y=-$\frac{5}{x}$图象上的是( )
| A. | (5,1) | B. | (1,5) | C. | (-1,5) | D. | (-5,-5) |
1.下列说法中,正确的是( )
| A. | 三角形的中线是射线 | B. | 三角形的三条高交于一点 | ||
| C. | 等腰三角形的三个内角相等 | D. | 三角形的三条角平分线交于一点 |
5.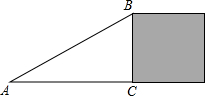 如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
 如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )| A. | 256cm | B. | 8cm | C. | 16cm | D. | 32cm |
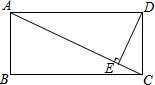 如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是3$\sqrt{2}$(结果用根号表示).
如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是3$\sqrt{2}$(结果用根号表示). 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AC=8,则CP的长为$\frac{8}{3}$.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点.若AC=8,则CP的长为$\frac{8}{3}$.