题目内容
16.如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(-5,0),且(n-3)2+$\sqrt{3m-12}$=0,点P从B出发,以每秒1个单位的速度沿射线BO匀速运动,设点P运动时间为t.(1)求A、C两点的坐标;
(2)连接PA,当△POA的面积等于△ABC的面积的一半时,求t的值;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出Q点坐标;若不存在,请说明理由.

分析 (1)由非负性先求出m,n即可求出点A,C坐标;
(2)根据点A,B,C的坐标求出△ABC的面积,再分点P在线段OB和射线OC上两种情况讨论计算;
(3)由∠POQ=∠AOC=90°,所以分两种情况讨论计算即可.
解答 t解:(1)∵(n-3)2+$\sqrt{3m-12}$=0
∴n-3=0,3m-12=0,
∴n=3,m=4,
∴A的坐标是(0,4),C的坐标是(3,0)
(2)∵B(-5,0),A(0,4),C(3,0);
∴OB=5,OC=3,OA=4
S△ABC=$\frac{1}{2}$OA×BC=$\frac{1}{2}$×4×8=16
①P在线段OB上,如图1,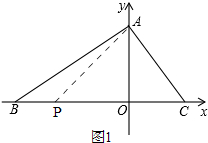
∵OP=5-t,OA=4
∴S△POA=$\frac{1}{2}$OP×AP=$\frac{1}{2}$(5-t)×4=16
∴t=1,
②当P在射线OC上如图2,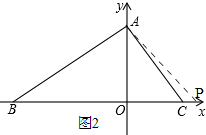
∵OP=t-5,OA=4,
∴S△POA=$\frac{1}{2}$OP×AP=$\frac{1}{2}$(5-t)×4=16
∴t=9
∴当t=1或t=9时,△POA的面积等于△ABCD的面积的一半;
(3)当P在线段BO上运动时,在y轴上存在点Q,使△POQ与△AOC全等,
①当BP=1,OQ=3时,△POQ和△AOC全等,
此时t=1,Q的坐标是(0,3)或(0,-3)
②当BP=2,OQ=4时,△POQ和△AOC全等,
此时t=2,Q的坐标是(0,4)或(0,-4);
综上所述,t=1或2时,Q的坐标是(0,3)或(0,4)或(0,3)或(0,4).
点评 此题是三角形综合题,主要考查了非负性,三角形的面积公式,全等三角形的性质,解本题的关键分情况讨论计算,也是解本题的难点.

练习册系列答案
相关题目
6.下列调查,适合用普查方式的是( )
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解中央电视台《新闻联播》的收视率 | |
| C. | 了解长江中鱼的种类 | |
| D. | 了解某班学生某次数学测验成绩 |
 ,则这辆车的实际牌照是81938.
,则这辆车的实际牌照是81938. 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OA的中点,⊙O的切线AF交DE的延长线于点F.
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OA的中点,⊙O的切线AF交DE的延长线于点F. (1)探究:已知,如图是一个三角形点阵,从上向下数有无数多行,其中第一行有一个点,第二行有两个点…第n行有n个点…容易发现,10是三角形点阵中前4行的点数和.
(1)探究:已知,如图是一个三角形点阵,从上向下数有无数多行,其中第一行有一个点,第二行有两个点…第n行有n个点…容易发现,10是三角形点阵中前4行的点数和.