题目内容
19. 如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E.
如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E.(1)依题意补全图形;
(2)猜想DE与BC的位置关系,并证明;
(3)若∠A=40°,∠ACD=35°,求∠CDB的度数.
分析 (1)画出∠CDE=∠ACD即可.
(2)结论:DE⊥BC,只要证明DE∥AC即可.
(3)由∠BDC=∠BDE+∠CDE,求出∠BDE,∠CDE即可解决问题.
解答 解:(1)梯形如图所示,
(2)结论:DE⊥BC.
理由:∵∠CDE=∠ACD,
∴AC∥DE,
∴∠DEB=∠ACB=90°.
∴DE⊥BC.
(3)∵AC∥DE,
∴∠BDE=∠A=40°,
∵∠CDE=∠ACD=35°,
∴∠CDB=∠BDE+∠CDE=75°.
点评 本题考查作图、平行线的判定和性质、三角形内角和定理等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
9.若n为整数且满足n<$\sqrt{43}$<n+1,那么n为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
11.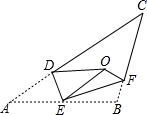 如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
 如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )
如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( )| A. | 40° | B. | 41° | C. | 42° | D. | 43° |
9. 如图为一条圆柱形排水管的横截面,已知圆心O到水面的距离OC是3dm,水面宽AB是8dm,排水管的截面的直径是( )
如图为一条圆柱形排水管的横截面,已知圆心O到水面的距离OC是3dm,水面宽AB是8dm,排水管的截面的直径是( )
 如图为一条圆柱形排水管的横截面,已知圆心O到水面的距离OC是3dm,水面宽AB是8dm,排水管的截面的直径是( )
如图为一条圆柱形排水管的横截面,已知圆心O到水面的距离OC是3dm,水面宽AB是8dm,排水管的截面的直径是( )| A. | 16dm | B. | 10dm | C. | 8dm | D. | 6dm |