题目内容
14.已知a,b是互质的正整数,满足a+b=2005,用[x]表示数x的整数部分,并记A=[$\frac{2005×1}{a}$]+[$\frac{2005×2}{a}$]+…+[$\frac{2005×a}{a}$],
B=[$\frac{2005×1}{b}$]+[$\frac{2005×2}{b}$]+…+[$\frac{2005×b}{b}$].
试求A+B的值.
分析 直接利用当a=2,则b=2003,当a=3,则b=2002,分别得出A+B的值,进而得出规律求出答案.
解答 解:当a=2,则b=2003,
故A=1002+2005=3007,
B=1+2+3+…+1001+1003+…+2003+2005
=$\frac{1002×1001}{2}$+$\frac{3006×1001}{2}$+2005
=501501+1504503+2005
=2008009,
则A+B=2011016,
当a=3,则b=2002,
A=668+1336+2005=4009,
B=1+…+667+669+…+1335+1337+…2003+2005
=222778+668334+1113890+2005
=20072007,
故A+B=2011016,
观察以上两种情况,可知,A+B=1+2+…+2003+2005×2=2011016,
所以,以此类推得到,A+B=2011016.
点评 此题主要考查了质数与取整计算,利用特殊值法求出A+B的值是解题关键.

练习册系列答案
相关题目
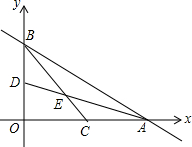 如图,直线y=-$\frac{1}{2}$x+2交x轴于A点,交y轴于B点,C、D分别为OA、OB的中点,连接AD、BC相交于E点.
如图,直线y=-$\frac{1}{2}$x+2交x轴于A点,交y轴于B点,C、D分别为OA、OB的中点,连接AD、BC相交于E点.
 如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E.
如图,三角形ABC中,∠C=90°,点D是AB上任意一点,∠CDE=∠ACD,DE交BC于点E. 如图,△ABC位于直角坐标系中,△ABC的三个顶点坐标分别为A(-3,5),B(-4,1),C(-1,3),点P(x,y)是△ABC内任一点,直线m上各点的横坐标都为1.
如图,△ABC位于直角坐标系中,△ABC的三个顶点坐标分别为A(-3,5),B(-4,1),C(-1,3),点P(x,y)是△ABC内任一点,直线m上各点的横坐标都为1.