题目内容
等腰三角形的腰长为13cm,底边长为10cm,求它的内切圆的半径.
考点:三角形的内切圆与内心,等腰三角形的性质
专题:
分析:等腰△ABC中,AB=AC=13,BC=10,AD为BC边上的高,根据等腰三角形的性质即可得D为BC中点,即BD=DC=5,求得高AD,进而求得△ABC的面积,即可求得内切圆的半径.
解答:解:等腰△ABC中,AB=AC,AD为BC边上的高,故AD为BC边上的中线,即BD=DC,
在直角△ABD中,AB=13,BD=5
∴AD=
=12,
则S△ABC=
×10×12=60cm2.
又∵S△ABC=
(13+13+10)r,
∴内切圆的半径r=
cm.
在直角△ABD中,AB=13,BD=5
∴AD=
| AB2-BD2 |
则S△ABC=
| 1 |
| 2 |
又∵S△ABC=
| 1 |
| 2 |
∴内切圆的半径r=
| 10 |
| 3 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了等腰三角形三线合一的性质,本题中正确的运用勾股定理求AD是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
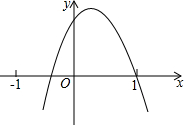 如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )
如图,抛物线y=ax2+bx+c的开口向下,交x轴的正半轴于(1,0),则下列结论错误的是( )| A、abc<0 |
| B、a-b+c<0 |
| C、2a+b>0 |
| D、a+c<0 |
 某校部分团员参加社会公益活动,准备购进一批玩具进行销售,并将所得利润捐给慈善机构.根据市场调查,这种玩具一段时间内的销售量y(个)于销售单价x(元∕个)之间的对应关系如图所示.
某校部分团员参加社会公益活动,准备购进一批玩具进行销售,并将所得利润捐给慈善机构.根据市场调查,这种玩具一段时间内的销售量y(个)于销售单价x(元∕个)之间的对应关系如图所示.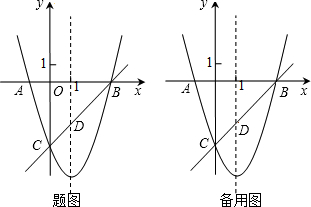
 已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2
已知,在正方形ABCD中,⊙O与正方形的边AB、AD相切,对角线BD交⊙O与M、N两点,且MN=2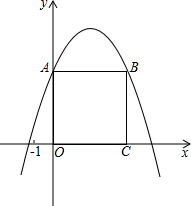 如图,正方形OCAB的顶点A、C分别在y轴、x轴上,正方形的边长为4,抛物线y=ax2+bx+c的图象经过A、B两点.下列说法中正确的个数有( )个
如图,正方形OCAB的顶点A、C分别在y轴、x轴上,正方形的边长为4,抛物线y=ax2+bx+c的图象经过A、B两点.下列说法中正确的个数有( )个 如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是
如图所示,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是