题目内容
19.计算:(1)计算:$4×{({-\frac{1}{36}})^0}-\sqrt{25}+{({\frac{1}{3}})^{-2}}$
(2)化简:(4ab3-8a2b2)÷(4ab)+2a(a-b)
分析 (1)原式利用零指数幂、负整数指数幂法则计算即可得到结果;
(2)原式利用多项式除以单项式,以及单项式乘以多项式法则计算即可得到结果.
解答 解:(1)原式=4-5+9=8;
(2)原式=b2-2ab+2a2-2ab=2a2-4ab+b2.
点评 此题考查了整式的除法,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.有x支球队参加篮球比赛,共比赛了21场,每两队之间都比赛一场,则下列方程中符合题意的是( )
| A. | x(x-1)=21 | B. | x(x+1)=21 | C. | x(x-1)=42 | D. | x(x+1)=42 |
7.在一个不透明的盒子里装有40个黑、白两种颜色的球,这些球除颜色外完全相同.小丽做摸球实验,搅匀后她从盒子里摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,表是实验中的一组统计数据:
若从盒子里随机摸出一个球,则摸到白球的概率的估计值为0.6.(精确到0.1)
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
4.要使分式$\frac{1}{a-3}$有意义,则a的取值应满足( )
| A. | a=3 | B. | a<3 | C. | a>3 | D. | a≠3 |
11.已知直线y-kx+k=0与直线ky+x-2k=0的交点在y轴上,则k的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
9.在下列调查中,适宜采用普查的是( )
| A. | 对我省七年级学生视力情况的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对量子通信卫星上零部件质量的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
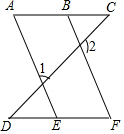 如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:
如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说: