题目内容
19.已知:在△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点P是BC边上的一个动点,连接AP.直线BE垂直于直线AP,交AP于点E,直线CF垂直于直线AP,交AP于点F.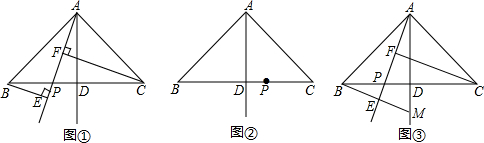
(1)当点P在BD上时(如图①),求证:CF=BE+EF;
(2)当点P在DC上时(如图②),CF=BE+EF还成立吗?若不成立,请画出图形,并直接写出CF、BE、EF之间的关系(不需要证明).
(3)若直线BE的延长线交直线AD于点M(如图③),找出图中与CP相等的线段,并加以证明.
分析 (1)如图①,先利用等角的余角相等得到∠ACF=∠BAE,则可根据“AAS”判定△ACF≌△BAE,得到AF=BE,CF=AE,由于AE=AF+EF,所以CF=BE+EF;
(2)如图②,与(1)一样可证明△ACF≌△BAE得到AF=BE,CF=AE而AE=AF-EF,易得CF=BE-EF;
(3)先判断△ABC为等腰直角三角形,由于点D是BC的中点,则AD⊥BC,再利用等角的余角相等得到∠1=∠3,则可根据“ASA”判判断△AEM≌△CFP,于是得到AM=CP.
解答 (1)证明: 如图①,
如图①,
∵AF⊥AP,BE⊥AP,
∴∠AFC=90°,∠AEB=90°,
∴∠CAF+∠ACF=90°,
而∠CAF+∠BAE=90°,
∴∠ACF=∠BAE,
在△ACF和△BAE中,
$\left\{\begin{array}{l}{∠AFC=∠BEA}\\{∠ACF=∠BAE}\\{AC=BA}\end{array}\right.$,
∴△ACF≌△BAE(AAS),
∴AF=BE,CF=AE,
而AE=AF+EF,
∴CF=BE+EF;
(2)解:CF=BE+EF不成立.
如图②,
与(1)一样可证明△ACF≌△BAE,
∴AF=BE,CF=AE,
而AE=AF-EF,
∴CF=BE-EF;
(3)CP=AM.理由如下:
∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
∵点D是BC的中点,
∴AD⊥BC,
∴∠ADC=90°,
∴∠1+∠2=90°,
∵∠3+∠2=90°,
∴∠1=∠3,
在△AEM和△CFP中,
$\left\{\begin{array}{l}{∠1=∠3}\\{AE=CF}\\{∠AEM=∠CFP}\end{array}\right.$,
∴△AEM≌△CFP(ASA),
∴AM=CP.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了等腰直角三角形的判定与性质.

| A. | 两直线平行,同旁内角相等 | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 三角形三条边的垂直平分线相交于一点,且这一点到三边的距离相等 | |
| D. | 两角分别相等且其中一组等角的对边相等的两个三角形全等 |
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
| A. | (-3,-1) | B. | (3,1) | C. | (-3,1) | D. | (-1,3) |
 如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( )
如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( ) 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.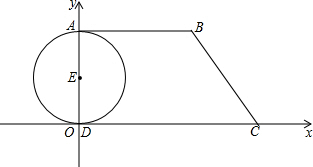 如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.