题目内容
9.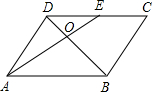 如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
如图,在?ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
分析 由AB∥CD,容易得出△AOB∽△EOD,又E为DC边的中点,AB=CD,故相似比为AB:ED=2:1,根据相似三角形的面积比等于相似比的平方,可求S△AOB.
解答 解:∵在?ABCD中,E为CD中点,
∴AB=CD=2DE,
又∵AB∥CD,
∴△AOB∽△EOD,
∴$\frac{{S}_{△AOB}}{{S}_{△DOE}}$=($\frac{AB}{DE}$)2=4,
∴S△AOB=4S△DOE=48cm2.
故选C.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质.关键是明确相似三角形的面积比等于相似比的平方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列事件是必然事件的是( )
| A. | 打开电视机,它正在播放动画片 | |
| B. | 播下一颗种子,种子一定会发芽 | |
| C. | 买100张中奖率为1%的彩票一定会中奖 | |
| D. | 太阳从东方升起 |
19.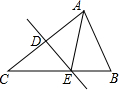 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |