题目内容
10．尺规作图，在数轴上画出$\sqrt{13}$，保留作图痕迹（用铅笔作图）．分析 根据勾股定理，作出以2和3为直角边的直角三角形，则其斜边的长即是$\sqrt{13}$；再以原点为圆心，以$\sqrt{13}$为半径画弧与数轴的正半轴的交点即为所求．
解答 解：所画图形如下所示，其中点A即为所求：
．
点评 本题考查勾股定理及实数与数轴的知识，要求能够正确运用数轴上的点来表示一个无理数，解题关键是构造直角三角形，并灵活运用勾股定理．
练习册系列答案
阅读快车系列答案
相关题目
5．
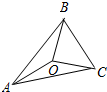如图，已知O是三角形ABC内一点，OA=OB=OC，∠ABC=70°，则∠AOC的大小为（ ）
如图，已知O是三角形ABC内一点，OA=OB=OC，∠ABC=70°，则∠AOC的大小为（ ）| A． | 70° | B． | 110° | C． | 140° | D． | 150° |
如图，在△ABC中，∠A=∠ACB，CD是△ABC的角平分线，CE是△ABC的高．
19．
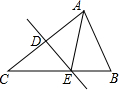如图，△ABC中，DE垂直平分AC，垂足为D，AD=3，△ABE的周长为13，那么△ABC的周长为（ ）
如图，△ABC中，DE垂直平分AC，垂足为D，AD=3，△ABE的周长为13，那么△ABC的周长为（ ）| A． | 10 | B． | 13 | C． | 16 | D． | 19 |
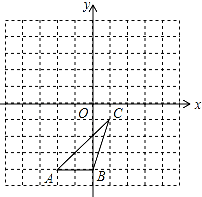如图，△ABC各顶点的坐标分别是A（-2，-4），B（0，-4），C（1，-1）