题目内容
14．
如图，已知△ABC的角平分线CD交AB于点D，DE∥BC交AC于点E，且DE=4，AE=3，则AC的长度为（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 根据角平分线的定义可得∠BCD=∠DCE，再根据两直线平行，内错角相等可得∠BCD=∠CDE，然后求出∠DCE=∠CDE，再根据等角对等边可得CE=DE，然后根据AC=AE+CE代入数据计算即可得解．
解答 解：∵CD是∠ACB的平分线，
∴∠BCD=∠DCE，
∵DE∥BC，
∴∠BCD=∠CDE，
∴∠DCE=∠CDE，
∴CE=DE，
∵DE=3，AE=4，
∴AC=AE+CE=4+3=7．
故选B．
点评 本题考查了等腰三角形的判定与性质，角平分线的定义，平行线的性质，熟记性质并求出CE=DE是解题的关键．
练习册系列答案
相关题目
5．
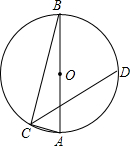如图，点C、D在以AB为直径的⊙O上，且CD平分∠ACB，若AB=6，∠CBA=15°，则CD的长是（ ）
如图，点C、D在以AB为直径的⊙O上，且CD平分∠ACB，若AB=6，∠CBA=15°，则CD的长是（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
2．万州区的出租车起步价是8元（2千米及2千米以内为起步价），以后每千米收费是1.6元，不足1千米按1千米收费，小明乘出租车到达目的地时计时器显示为14.4元，则此出租车行驶的路程可能为（ ）
| A． | 6.9千米 | B． | 5.5千米 | C． | 4.1千米 | D． | 3.5千米 |
9．
如图，在平面直角坐标系中，⊙O的半径为1，且与y轴交于点B，过点B作直线BC平行于x轴，点M（a，1）在直线BC上，若在⊙O上存在点N，使得∠OMN=45°，则a的取值范围是（ ）
如图，在平面直角坐标系中，⊙O的半径为1，且与y轴交于点B，过点B作直线BC平行于x轴，点M（a，1）在直线BC上，若在⊙O上存在点N，使得∠OMN=45°，则a的取值范围是（ ）| A． | -1≤a≤1 | B． | -$\frac{1}{2}$$≤a≤\frac{1}{2}$ | C． | $-\sqrt{2}≤a≤\sqrt{2}$ | D． | $-\frac{\sqrt{2}}{2}≤a≤\frac{\sqrt{2}}{2}$ |
如图，∠AOC和∠BOD是直角，如果∠AOB=120°，那么∠COD为60°．