Question

8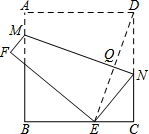．如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是（　　）

• A． 4cm
• B． 2cm
• C． $\sqrt{2}$cm
• D． 1cm

Answer 1

分析 如图，取AB、CD中点K、G，连接KG、BD交于点O，根据点Q运动的路线就是线段OG即可解决问题．

解答 解：如图，取AB、CD中点K、G，连接KG、BD交于点O．

由题意可知点Q运动的路线就是线段OG，
∵DO=OB，DG=GC，
∴OG=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2．
∴点Q移动路线长度的最大值是2．
故选B．

点评 本题考查轨迹、翻折变换、三角形中位线定理等知识，解题的关键是找到点Q的运动路线，属于中考常考题型．