题目内容
17．
已知：如图，E是BC上一点，AB=EC，AB∥CD，BC=CD．求证：AC=ED．
分析 根据两直线平行，内错角相等可得∠B=∠ECD，然后利用“边角边”证明△ABC和△ECD全等，再根据全等三角形对应边相等即可得证．
解答 证明：∵AB∥CD，
∴∠B=∠DCE．
在△ABC和△ECD中，
$\left\{\begin{array}{l}{AB=EC}\\{∠B=∠DCE}\\{BC=CD}\end{array}\right.$
∴△ABC≌△ECD（SAS）．
∴AC=ED．
点评 本题考查了三角形全等的判定与性质，平行线的性质，比较简单，求出∠B=∠ECD是证明三角形全等的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
7．判断下列说法错误的是（ ）
| A． | 2是8的立方根 | B． | ±4是64的立方根 | ||
| C． | -$\frac{1}{3}$是-$\frac{1}{27}$的立方根 | D． | （-4）3的立方根是-4 |
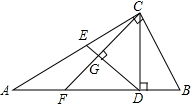如图，Rt△ABC中，∠C=90°，∠A=30°，BC=2，CD是斜边AB上的高，点E为边AC上一点（点E不与点A、C重合），连接DE，作CF⊥DE，CF与边AB、线段DE分别交于点F，G；