题目内容
9.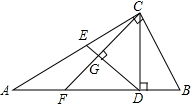 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,CD是斜边AB上的高,点E为边AC上一点(点E不与点A、C重合),连接DE,作CF⊥DE,CF与边AB、线段DE分别交于点F,G;
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,CD是斜边AB上的高,点E为边AC上一点(点E不与点A、C重合),连接DE,作CF⊥DE,CF与边AB、线段DE分别交于点F,G;(1)求线段CD、AD的长;
(2)设CE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
分析 (1)利用特殊角的三角函数可知sin∠B=$\frac{CD}{BC}$,tan∠A=$\frac{CD}{AD}$,由此求得线段CD、AD的长;
(2)证得△CDE∽△BFC,得出$\frac{CE}{BC}$=$\frac{CD}{BF}$,整理得出答案即可.
解答 解:(1)在Rt△BCD中,
BC=2,∠B=90°-∠A=60°,
sin∠B=$\frac{CD}{BC}$,
即CD=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
同理tan∠A=$\frac{CD}{AD}$,
AD=$\frac{\sqrt{3}}{tan30°}$=3;
(2)∵∠CDE=∠BFC=90°-∠DCF,
∠ECD=∠B=60°,
∴△CDE∽△BFC,
∴$\frac{CE}{BC}=\frac{CD}{BF}$,
即$\frac{x}{2}=\frac{{\sqrt{3}}}{y+1}$,
∴$y=\frac{{2\sqrt{3}}}{x}-1$,($\frac{{\sqrt{3}}}{2}≤x<2\sqrt{3}$).
点评 此题考查相似的综合题,综合考查了特殊角的三角函数,相似三角形的判定与性质,注意分类讨论思想的渗透.

练习册系列答案
相关题目
19.甲、乙两个兴趣小组参加了某次知识竞赛,辅导老师对两个小组竞赛成绩进行了统计,得到以下数据:$\overline{{x}_{甲}}$=79,$\overline{{x}_{乙}}$=82,S甲2=82,S乙2=79,则这两个小组成员的成绩比较稳定的是( )
| A. | 甲组 | B. | 乙组 | C. | 两组一样 | D. | 无法确定 |
19.实数-2的绝对值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -2 |
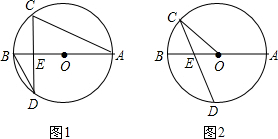
 已知:如图,E是BC上一点,AB=EC,AB∥CD,BC=CD.求证:AC=ED.
已知:如图,E是BC上一点,AB=EC,AB∥CD,BC=CD.求证:AC=ED.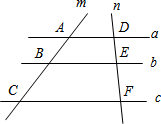 如图,直线a∥b∥c,直线m、n与a、b、c分别交于点A、B、C、D、E、F,若AB=6,DE=3,EF=4,则BC=8.
如图,直线a∥b∥c,直线m、n与a、b、c分别交于点A、B、C、D、E、F,若AB=6,DE=3,EF=4,则BC=8.