题目内容
18.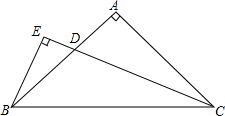 如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.
如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.
分析 延长BE、CA交与点F,根据等角的余角相等求出∠ACD=∠ABF,再利用“角边角”证明△AFB≌△ADC;可得CD=BF,利用“SAS”证明△BCE和△FCE全等,根据全等三角形得出∠BCE=∠FCE即可.
解答 证明:如图,
∵BE⊥CD,∠BAC=90°,
∴∠ACD+∠F=180°-90°=90°,
∠ABF+∠F=180°-90°=90°,
∴∠ACD=∠ABF,
在△AFB和△ADC中,
$\left\{\begin{array}{l}{∠ACD=∠ABF}\\{AB=AC}\\{∠CAD=∠BAF}\end{array}\right.$,
∴△AFB≌△ADC(ASA);
∴CD=BF,
∵EB=$\frac{1}{2}$DC=$\frac{1}{2}$BF,
∴BE=EF,
在△BCE和△FCE中,
$\left\{\begin{array}{l}{CE=CE}\\{∠CEB=∠CEF}\\{BE=EF}\end{array}\right.$,
∴△BCE≌△FCE(ASA),
∴∠BCE=∠FCE,
∴CD平分∠ACB.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的证明方法,正确作出辅助线,并准确识图是解题的关键.

练习册系列答案
相关题目
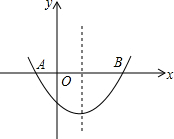 如图,抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和B(3,0),顶点坐标是(1,-2),观察图形回答下列问题:
如图,抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和B(3,0),顶点坐标是(1,-2),观察图形回答下列问题:
 如图,已知AB=CB,AD=CD,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知AB=CB,AD=CD,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.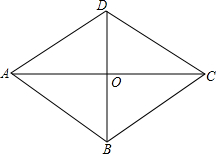 如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:
如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒: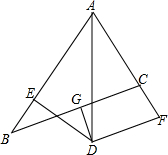 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.