题目内容
6．
如图，已知AB=CB，AD=CD，点P在BD上，PM⊥AD于M，PN⊥CD于N，求证：PM=PN．
分析 由已知容易求证△ADB≌△CDB（SSS），可得∠ADB=∠CDB，再根据角平分线性质的逆定理，可证PM=PN．
解答 证明：在△ADB与△CDB中，
$\left\{\begin{array}{l}{AB=CB}\\{AD=CD}\\{DB=DB}\end{array}\right.$，
∴△ADB≌△CDB（SSS），
∴∠ADB=∠CDB，
∵PM⊥AD于M，PN⊥CD于N，
∴PM=PN．
点评 本题主要考查角平分线性质定理及其逆定理，由已知能够注意到△ADB≌△CDB是解决的关键．
练习册系列答案
阅读快车系列答案
相关题目
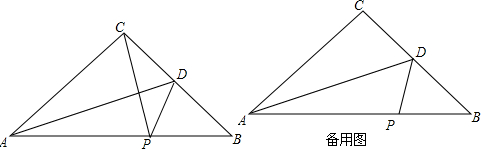
如图，在△ABC中，AB=3，AC=5，AD是边BC上的中线，AD=ED=2，求△ABC的面积．
如图，△ABC，△ADE均为等边三角形，连接BD，CE，则线段BD与CE的数量关系是BD=CE．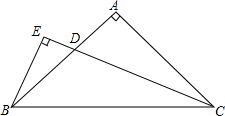
如图，△ABC中，AB=AC，∠BAC=90°，EB=$\frac{1}{2}$DC，BE⊥CD，垂足E在CD的延长线上，求证：CD平分∠ACB．
16．抛物线y=-$\frac{1}{4}{（{x-\frac{1}{2}}）^2}$-5的顶点坐标是（ ）
| A． | $（\frac{1}{2}，-5）$ | B． | $（-5，-\frac{1}{2}）$ | C． | $（-\frac{1}{2}，-5）$ | D． | $（-\frac{1}{2}，5）$ |