题目内容
8.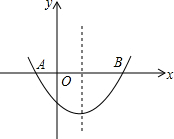 如图,抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和B(3,0),顶点坐标是(1,-2),观察图形回答下列问题:
如图,抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和B(3,0),顶点坐标是(1,-2),观察图形回答下列问题:(1)AB=4;
(2)当x=1时,y的值最小,最小值是-2;
(3)当x<-1或x>3时,y>0;
(4)当x<1时,y随x的增大而减小;
(5)该抛物线的解析式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.
分析 (1)用B点的横坐标减去A点的横坐标即可得到AB的长;
(2)根据二次函数的性质,由抛物线的顶点坐标可判断函数的最小值;
(3)观察函数图象,写出函数图象在x轴上方所对应的自变量的范围即可;
(4)根据二次函数的性质求解;
(5)利用待定系数法求二次函数解析式.
解答 解:(1)AB=3-(-1)=4;
(2)∵抛物线的顶点为(1,-2),
∴当x=1,y有最小值-2;
(3)观察图象得当x<-1或x>3时,y>0;
(4)∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x的增大而减小;
(5)设抛物线的解析式为y=a(x+1)(x-3),
把(1,-2)代入得a•2•(-2)=-2,解得a=$\frac{1}{2}$,
抛物线的解析式为y=$\frac{1}{2}$(x+1)(x-3),即y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.
故答案为4;1,-2;-1,3;<1;y=$\frac{1}{2}$x2-x-$\frac{3}{2}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;从二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了二次函数的性质.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.布袋中有3个红球和2个白球,它们除颜色外其余都相同,如果从布袋中随机摸出一个球,那么所摸到的球恰好是红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
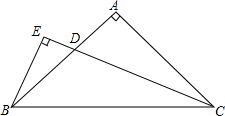 如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.
如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.