题目内容
3.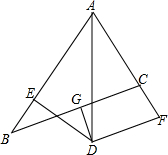 如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DG交于点D,过D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.(1)求证:BE=CF;
(2)若AB=a,AC=b,求AE,BE的长.
分析 (1)连接BD,CD.利用垂直平分线的性质得出DB=DC,证得Rt△DCF≌Rt△DBE,得出结论;
(2)首先证得Rt△AED≌Rt△AFD,得到AE=AF,然后利用(1)结论,根据线段的和与差得出答案即可.
解答  (1)证明:连接BD,CD,
(1)证明:连接BD,CD,
∵点D在BC的垂直平分线上,
∴DB=DC,
∵点D在∠BAC的平分线上,DE⊥AB,DF⊥AC,
∴DE=DF.
在Rt△DCF与Rt△DBE中,
$\left\{\begin{array}{l}{DE=DF}\\{DB=DC}\end{array}\right.$,
∴Rt△DCF≌Rt△DBE(HL),
∴CF=BE;
(2)解:∵点D在∠BAC的平分线上,DE⊥AB,DF⊥AC,
∴DE=DF.
在Rt△AED与Rt△AFD中,
$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AB=a,AC=b,CF=BE,AE=AF=AC+CF=AC+BE,
∴AE-BE=AC=b,
∵AE+BE=AB=a,
∴BE=$\frac{1}{2}$(a-b),
∴AE=$\frac{1}{2}$(a+b).
点评 此题考查三角形全等的判定与性质,角平分线的性质,线段垂直平分线的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
8.下面各组中的三条线段能组成三角形的是( )
| A. | 6cm,7cm,12cm | B. | 6cm,8cm,15cm | C. | 8cm,12cm,20cm | D. | 6cm,6cm,13cm |
13.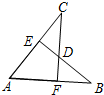 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.
以上结论正确的( )
 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.
以上结论正确的( )
| A. | 只有① | B. | 只有② | C. | 只有③ | D. | 有①和②和③ |
 如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积.
如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积. 如图,△ABC,△ADE均为等边三角形,连接BD,CE,则线段BD与CE的数量关系是BD=CE.
如图,△ABC,△ADE均为等边三角形,连接BD,CE,则线段BD与CE的数量关系是BD=CE.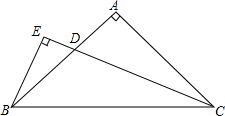 如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.
如图,△ABC中,AB=AC,∠BAC=90°,EB=$\frac{1}{2}$DC,BE⊥CD,垂足E在CD的延长线上,求证:CD平分∠ACB.