题目内容
13.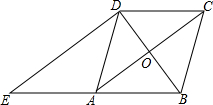 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
分析 (1)根据平行四边形的判定证明即可;
(2)利用平行四边形的性质得出平行四边形的周长即可.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,
∴AE∥CD,∠AOB=90°,
∵DE⊥BD,即∠EDB=90°,
∴∠AOB=∠EDB,
∴DE∥AC,
∴四边形ACDE是平行四边形;
(2)解:∵四边形ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5,
∵四边形ACDE是平行四边形,
∴AE=CD=5,DE=AC=8,
∴△ADE的周长为AD+AE+DE=5+5+8=18.
点评 此题考查平行四边形的性质和判定问题,关键是根据平行四边形的判定解答即可.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
3.当1≤x≤4时,mx-4<0,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m>4 | D. | m<4 |
4. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
 如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )| A. | 35° | B. | 95° | C. | 85° | D. | 75° |
18.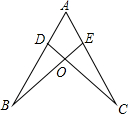 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )| A. | ∠B=∠C | B. | AD=AE | C. | BD=CE | D. | BE=CD |
2.下列计算中,结果是a6的是( )
| A. | a2+a4 | B. | a2•a3 | C. | a12÷a2 | D. | (a2)3 |
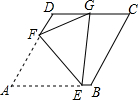 如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=$\frac{7\sqrt{21}}{20}$.
如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=$\frac{7\sqrt{21}}{20}$.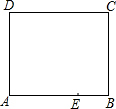 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.
如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.