题目内容
8.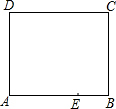 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.
如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5$\sqrt{2}$或4$\sqrt{5}$或5.
分析 分情况讨论:①当AP=AE=5时,则△AEP是等腰直角三角形,得出底边PE=$\sqrt{2}$AE=5$\sqrt{2}$即可;
②当PE=AE=5时,求出BE,由勾股定理求出PB,再由勾股定理求出等边AP即可;
③当PA=PE时,底边AE=5;即可得出结论.
解答 解:如图所示: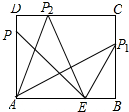
①当AP=AE=5时,
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=$\sqrt{2}$AE=5$\sqrt{2}$;
②当PE=AE=5时,
∵BE=AB-AE=8-5=3,∠B=90°,
∴PB=$\sqrt{P{E}^{2}-B{E}^{2}}$=4,
∴底边AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$;
③当PA=PE时,底边AE=5;
综上所述:等腰三角形AEP的对边长为5$\sqrt{2}$或4$\sqrt{5}$或5;
故答案为:5$\sqrt{2}$或4$\sqrt{5}$或5.
点评 本题考查了矩形的性质、等腰三角形的判定、勾股定理;熟练掌握矩形的性质和等腰三角形的判定,进行分类讨论是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图所示的几何体,它的左视图与俯视图都正确的是( )
如图所示的几何体,它的左视图与俯视图都正确的是( )
 如图所示的几何体,它的左视图与俯视图都正确的是( )
如图所示的几何体,它的左视图与俯视图都正确的是( )| A. |  | B. |  | C. |  | D. |  |
3.若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( )
| A. | ab>0 | B. | a-b>0 | C. | a2+b>0 | D. | a+b>0 |
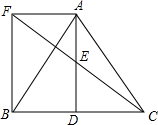 如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.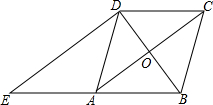 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.