题目内容
12.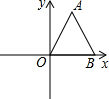 如图,在直角坐标系中,△OAB是等边三角形,点A的坐标为(1,$\sqrt{3}$),则点B关于y轴对称的点坐标为(-2,0).
如图,在直角坐标系中,△OAB是等边三角形,点A的坐标为(1,$\sqrt{3}$),则点B关于y轴对称的点坐标为(-2,0).
分析 先过点A作AC⊥OB,根据△AOB是等边三角形,求出OA=OB,OC=BC,∠AOB=60°,再根据点B的坐标,求出OB的长,再根据勾股定理求出AC的值,从而得出点A的坐标.
解答  解:过点A作AC⊥OB,
解:过点A作AC⊥OB,
∵△AOB是等边三角形,
∴OA=OB,OC=BC,
∠AOB=60°,
∵点A的坐标为(1,$\sqrt{3}$),
∴AC=$\sqrt{3}$,OC=1,
∴OB=2OC=2,
∴B(2,0),
∴点B关于y轴对称的点坐标为(-2,0).
故答案为:(-2,0).
点评 此题考查了等边三角形的性质,用到的知识点是勾股定理,关键是作出辅助线,求出点B的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.如图,正确画出△ABC中边AC上高的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.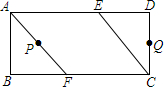 如图,长方形ABCD中,AB=4cm,BC=9cm,点E、F分别在AD、BC上,且BF=DE=3cm,连接AF、CE.
如图,长方形ABCD中,AB=4cm,BC=9cm,点E、F分别在AD、BC上,且BF=DE=3cm,连接AF、CE.