题目内容
7.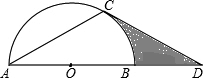 如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
分析 连接OC,求出∠D和∠COD,求出边DC长,分别求出三角形OCD的面积和扇形COB的面积,即可求出答案.
解答 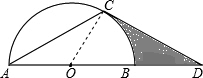 解:连接OC,
解:连接OC,
∵AC=CD,∠ACD=120°,
∴∠CAD=∠D=30°,
∵DC切⊙O于C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠COD=60°,
在Rt△OCD中,∠OCD=90°,∠D=30°,OC=2,
∴CD=2$\sqrt{3}$,
∴阴影部分的面积是S△OCD-S扇形COB=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π,
故答案为:2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了等腰三角形性质,三角形的内角和定理,切线的性质,扇形的面积,三角形的面积的应用,解此题的关键是求出扇形和三角形的面积,题目比较典型,难度适中.

练习册系列答案
相关题目
18.下列函数中,y随x增大而减小的是( )
| A. | y=$\frac{3}{x}$ | B. | y=2x+5 | C. | y=$\frac{1}{2}$x2 (x<-2) | D. | y=$\frac{1}{2}$x2(x>0) |
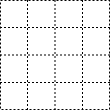 如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.
如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.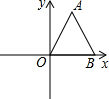 如图,在直角坐标系中,△OAB是等边三角形,点A的坐标为(1,$\sqrt{3}$),则点B关于y轴对称的点坐标为(-2,0).
如图,在直角坐标系中,△OAB是等边三角形,点A的坐标为(1,$\sqrt{3}$),则点B关于y轴对称的点坐标为(-2,0). 如图共有24个三角形.
如图共有24个三角形.
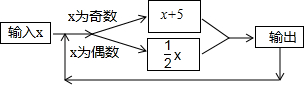 如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2013次输出的结果为6.
如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2013次输出的结果为6.