题目内容
15.已知△ABC和△DEF关于直线对称,若△ABC的周长为40cm,△DEF的面积为60cm2,DE=8cm,则△DEF的周长为40cm,△ABC的面积为60cm2,AB边上的高为15cm.分析 根据关于直线对称的两个三角形全等,再根据全等三角形的周长相等,面积相等,对应边相等解答.
解答 解:∵△ABC和△DEF关于直线对称,
∴△ABC≌△DEF,
∴△ABC的周长为40cm,△DEF的面积为60cm2,DE=8cm,
∴△DEF的周长为40cm,△ABC的面积为60cm2,AB=DE=8cm,
∵$\frac{1}{2}$•AB•h=60,即$\frac{1}{2}$×8×h=60,
∴h=15,即AB边上的高为15cm.
故答案为:40cm,60cm2,15cm.
点评 本题考查了轴对称的性质,全等三角形的性质,熟记关于直线对称的两个三角形全等是解题的关键.

练习册系列答案
相关题目
5.两个相似三角形的相似比为7:5,则下列说法正确的是( )
| A. | 面积比是7:5 | B. | 周长比是49:25 | ||
| C. | 对应边上的高之比为 7:5 | D. | 对应边上的中线之比为49:25 |
6.已知抛物线y=(m+1)x${\;}^{{m^2}+m}}$有最高点,则m的值是( )
| A. | m<-1 | B. | m=1 | C. | m=-2 | D. | m=1或m=-2 |
3.下列函数中,是二次函数的是( )
| A. | y=2x | B. | y=${x^2}+\frac{1}{x}$ | C. | y=$\sqrt{{x}^{2}-2x+1}$ | D. | y=x2-2 |
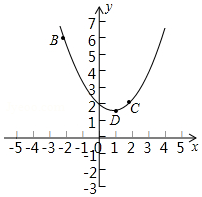 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.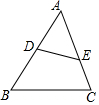 如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.
如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.