题目内容
7.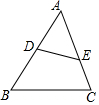 如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.
如图,在△ABC中,D、E分别是AB、AC上的点,在下列条件中:①∠AED=∠B;②$\frac{AD}{AC}$=$\frac{AE}{AB}$;③$\frac{DE}{BC}$=$\frac{AD}{AC}$,能够判断△ADE与△ACB相似的是①②.
分析 根据图形得到∠A是公共角,然后根据相似三角形的判定方法进行判断即可.
解答 解:由图可知,∠A是△ADE与△ACB的公共角,
①∠AED=∠B可以利用“两组角对应相等,两三角形相似”得到△ADE与△ACB相似;
②$\frac{AD}{AC}$=$\frac{AE}{AB}$可以利用“两边对应成比例,夹角相等,两三角形相似”得到△ADE与△ACB相似;
③$\frac{DE}{BC}$=$\frac{AD}{AC}$,公共角不是夹角,不能得到△ADE与△ACB相似;
综上所述,能判断△ADE与△ACB相似的是①②.
故答案为:①②.
点评 本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解题的关键,要注意∠A是两三角形的公共角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列计算错误的是( )
| A. | $\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}$=$\frac{a}{b}$ | B. | $\frac{(a-b)^{2}}{b-a}$=a-b | ||
| C. | $\frac{{m}^{2}-2m}{4-{m}^{2}}$=-$\frac{m}{m+2}$ | D. | $\frac{0.2a+b}{0.5a-b}$=$\frac{2a+10b}{5a-10b}$ |
12.小明带50元去买单价为3元的笔记本,则他所花的钱y(元)与他买这种笔记本的本数x之间的关系式是( )
| A. | y=3x | B. | y=3x-50 | C. | y=50-3x | D. | y=50+3x |
19.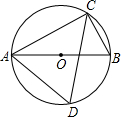 如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
 如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )| A. | 25 | B. | 30° | C. | 45° | D. | 65° |
17.如图所示,数轴的单位长度为1,如果点M、N表示的数的绝对值相等,那么点M表示的数是( )


| A. | -4 | B. | -3 | C. | -2 | D. | 3 |
 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2=6.