题目内容
7.已知有理数x,y,z满足(|x+1|+|x-2|)(|y-1|+|y-3|)(|z-1|+|z+2|)=18,求x+2y+3z的最大值与最小值.分析 根据绝对值的性质分别得出|x+1|+|x-2|,|y-1|+|y-3|,|z-1|+|z+2|的取值范围,进而得出x,y,z的取值范围进而得出答案.
解答 解:当x<-1时,y=-(x+1)-(x-2)=-2x+1>3,
当-1≤x≤2时,y=x+1-(x-2)=3,
当x>2时,y=x+1+x-2=2x-1>3,
所以可知|x+1|+|x-2|≥3,
同理可得:
|y-1|+|y-3|≥2,
|z-1|+|z+2|≥3,
所以(|x+1|+|x-2|)(|y+1|+|y-2|)(|z-3|+|z+1|)≥2×3×3=18,
所以|x+1|+|x-2|=3,
|y-1|+|y-3|=2,
|z-1|+|z+2|=3,
所以-1≤x≤2,
1≤y≤3,
-2≤z≤1,
∴x+2y+3z的最大值为:2+2×3+3×1=11,
最小值为:-1+2×1+3×(-2)=-5.
点评 此题主要考查了绝对值的性质,根据题意得出x,y,z的取值范围是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.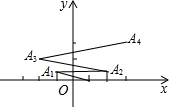 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )| A. | (50,49) | B. | (51,50) | C. | (-50,49) | D. | (100,99) |
19.一个等腰三角形的一边长是6,另一边长是8.那么这个等腰三角形的周长是( )
| A. | 20 | B. | 20或24 | C. | 22 | D. | 20或22. |
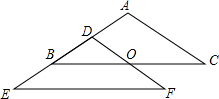 如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.
如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.