题目内容
4.已知,□ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.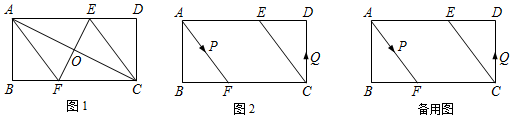
(1)如图1,连接AF、CE.求证:四边形AFCE为平行四边形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
分析 (1)①先证明四边形ABCD为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;
②根据勾股定理即可求AF的长;
(2)分情况讨论可知,P点在BF上,Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
∵EF垂直平分AC,
∴OA=OC.
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠CAD=∠ACB}\\{∠AEF=∠CFE}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS),
∴OE=OF(AAS).
∵EF⊥AC,
∴四边形AFCE为菱形.即四边形AFCE为平行四边形.
②设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,由勾股定理,得
16+(8-x)2=x2,
解得:x=5,
∴AF=5.
(2)由作图可以知道,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
∴PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=t,QA=12-0.8t,
∴t=12-0.8t,
解得:t=$\frac{20}{3}$.
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=$\frac{20}{3}$秒.
点评 本题考查了矩形的性质的运用,菱形的判定及性质的运用,勾股定理的运用,平行四边形的判定及性质的运用,解答时分析清楚动点在不同的位置所构成的图形的形状是解答本题的关键.

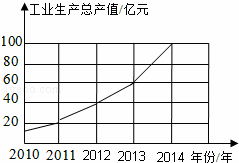 如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )
如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )| A. | 2010年至2014年间工业生产总值逐年增加 | |
| B. | 2014年的工业生产总值比前一年增加了40亿元 | |
| C. | 2012年与2013年每一年与前一年比,其增长额相同 | |
| D. | 从2011年至2014年,每一年与前一年比,2014年的增长率最大 |
| A. | m2+m2=m4 | B. | (m+1)2=m2+1 | C. | (3mn2)2=6m2n4 | D. | 2m2n÷(-mn)=-2m |
 在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间t(时)变化的图象(全程)如图所示.有下列说法中正确的说法有( )
在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间t(时)变化的图象(全程)如图所示.有下列说法中正确的说法有( )①起跑后1小时内,甲在乙的前面;
②第1小时甲跑了10千米,乙跑了8千米;
③乙的行程y与时间t的关系式为y=10t;
④第1.5小时,甲跑了12千米.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 9.8×103 | B. | 9.8×104 | C. | 0.98×104 | D. | 98.0×102 |
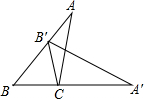 如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时,点A的对应点A′恰好落在BC边的延长线上,下列结论错误的是( )
如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时,点A的对应点A′恰好落在BC边的延长线上,下列结论错误的是( )| A. | ∠BCB′=∠ACA′ | B. | ∠ACB=2∠B | C. | ∠B′CA=∠B′AC | D. | B′C平分∠BB′A′ |
 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )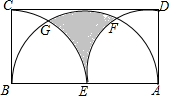 如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8}{3}$π.
如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8}{3}$π.