Question

14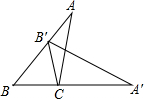．如图，将△ABC绕点C顺时针旋转，使点B落在AB边上点B′处，此时，点A的对应点A′恰好落在BC边的延长线上，下列结论错误的是（　　）

• A． ∠BCB′=∠ACA′
• B． ∠ACB=2∠B
• C． ∠B′CA=∠B′AC
• D． B′C平分∠BB′A′

Answer 1

分析 根据旋转的性质得到∠BCB′=∠ACA′，故A正确，根据等腰三角形的性质得到∠B=∠BB'C，根据三角形的外角的性质得到∠A'CB'=2∠B，等量代换得到∠ACB=2∠B，故B正确；等量代换得到∠A′B′C=∠BB′C，于是得到B′C平分∠BB′A′，故D正确．

解答 解：根据旋转的性质得，∠BCB'和∠ACA'都是旋转角，则∠BCB′=∠ACA′，故A正确，
∵CB=CB'，
∴∠B=∠BB'C，
又∵∠A'CB'=∠B+∠BB'C，
∴∠A'CB'=2∠B，
又∵∠ACB=∠A'CB'，
∴∠ACB=2∠B，故B正确；
∵∠A′B′C=∠B，
∴∠A′B′C=∠BB′C，
∴B′C平分∠BB′A′，故D正确；
故选C．

点评 本题考查了旋转的性质，角平分线的定义，等腰三角形的性质，正确的识别图形是解题的关键．