Question

19．如图，在△ABC中，∠ABC=90°，AB=12，BC=5，若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（　　）

• A． 9
• B． 10
• C． 12
• D． 13

Answer 1

分析 根据三角形中位线定理求出DE，得到DF∥BM，再证明EC=EF=$\frac{1}{2}$AC，由此即可解决问题．

解答 解：在Rt△ABC中，∵∠ABC=90°，AB=12，BC=5，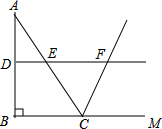
∴AC=13，
∵DE是△ABC的中位线，
∴DF∥BM，DE=$\frac{1}{2}$BC=$\frac{5}{2}$，
∴∠EFC=∠FCM，
∵∠FCE=∠FCM，
∴∠EFC=∠ECF，
∴EC=EF=$\frac{1}{2}$AC=$\frac{13}{2}$，
∴DF=DE+EF=9．
故选A．

点评 本题考查三角形中位线定理、等腰三角形的判定和性质、勾股定理等知识，解题的关键是灵活应用三角形中位线定理，掌握等腰三角形的判定和性质．